Contents
都立青山の大問4を解く上でのポイント
- 円周角の定理
- 三平方の定理
- 空間図形を展開する能力
- 相似
が重要です。
〔問1〕この問題は1,2分で解けるようにしましょう!
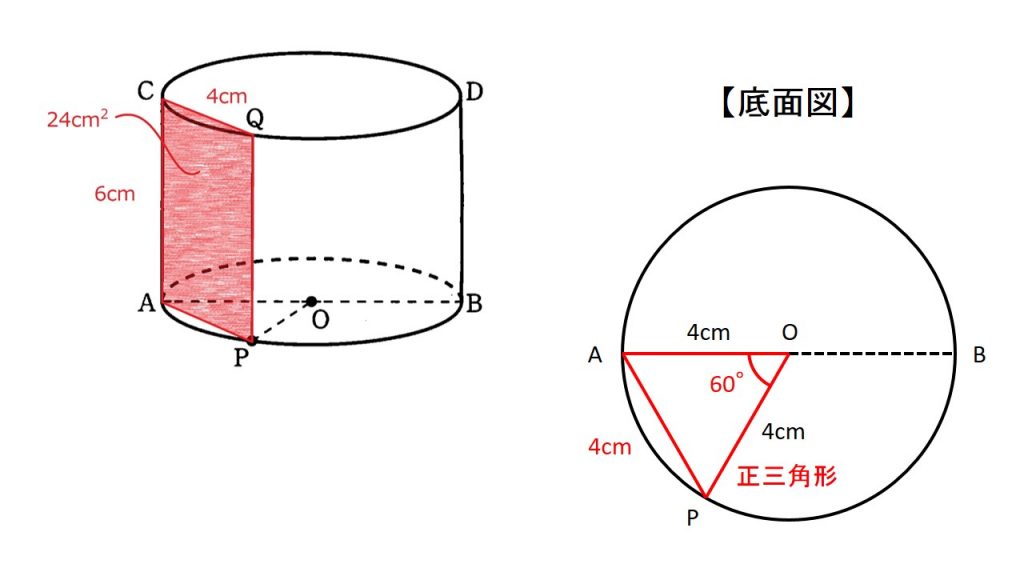
四角形APQCの面積が24cm2と与えられていることを利用して∠AOPを求めます.
まずは四角形APQCの面積が24cm2と線分CAが6cmであることから線分APが4cm.
よって△AOPは1辺4cmの正三角形になるため,∠AOP=60°.
〔問2〕(1)5分程度で解けるといいと思います!また途中式も丁寧に!
四角錐R-PBDQがどのような図形になるか理解すればこの問題は解けます.
【ヒント】
円周角の定理より∠PBR=90°,円柱より∠RBD=90°となることがわかります.
よって四角錐R-PBDQの底面が四角形PBDQ,高さが線分RBとなり,体積が求まります.
【詳しい解説】
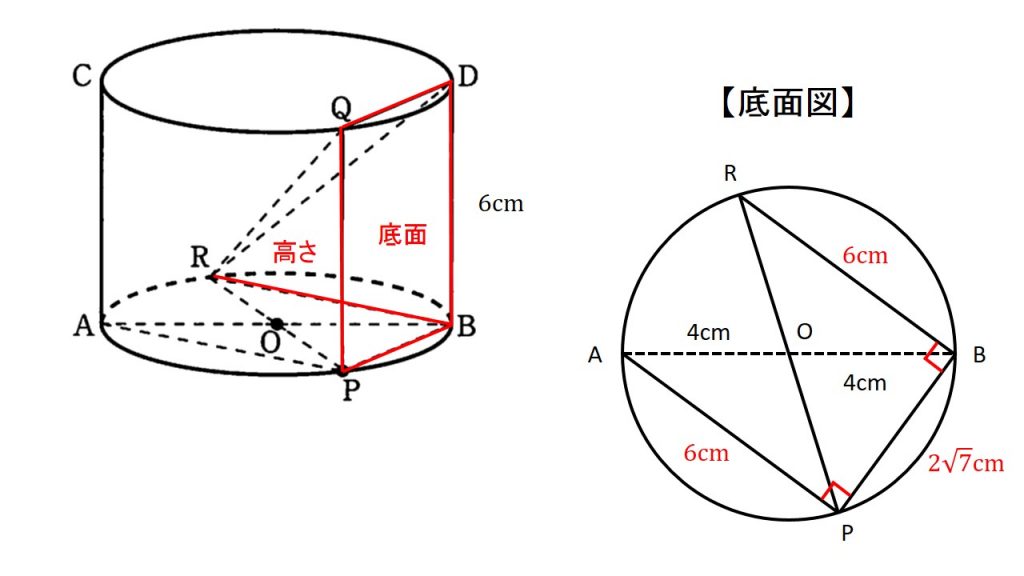
線分PRが円の直径から円周角の定理より∠PBR=90°.
円柱なので∠RBD=90°.
上記より,四角錐の体積は底面PBDQと高さRBで求まります.
まずは底面積を求めます.
線分ABも直径より∠APB=90°になり,三平方の定理より
$$\rm PB=2\sqrt{7}[cm]$$.
したがって
$$\rm (底面積)=6\times2\sqrt{7}=12\sqrt{7}[cm^{2}]$$
高さRBは四角形APBRが長方形であることからRB=AP=6cm.
ゆえに
$$\rm (四角錐の体積)=(底面)\times(高さ)\times\frac{1}{3}\\=24\sqrt{7}[cm^{3}]$$
〔問2〕(2)7分程度で解けると良いと思います!
展開図と中心角を利用した相似比をしっかり理解していれば解けます.
【ヒント】
最短の線lが見えるように展開図を書き,点P, R, S, Tの位置がわかればこの問題は解けます.
【詳しい解説】
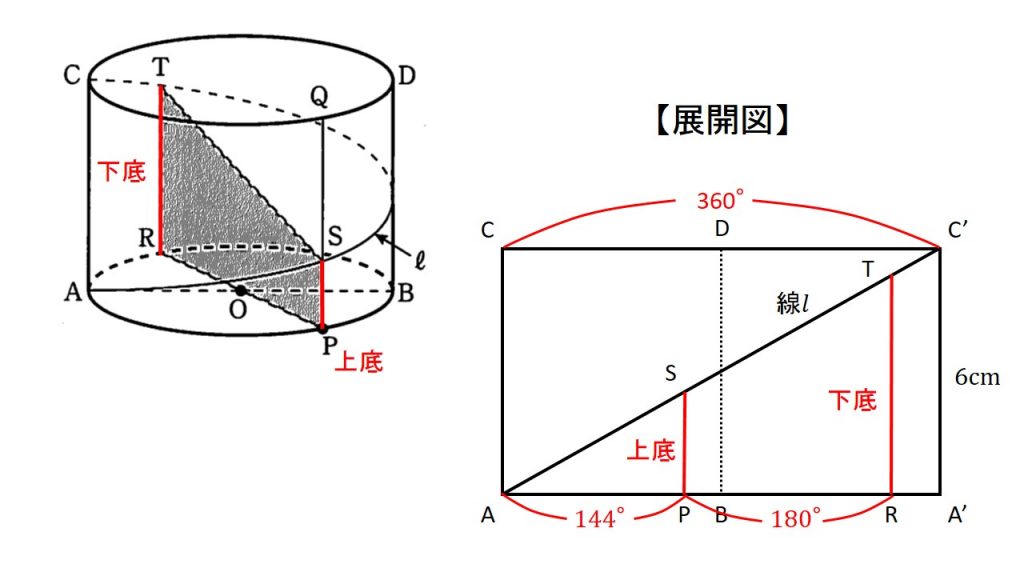
四角形PSTRが台形であることがわかることから上底SPと下底TRの長さを求めれば面積が求まります.
では上底と下底をどのようにして求めるか考えます.
空間図形における最短距離の問題は必ず展開図を疑います.
もちろんこの問題でも展開図を用います.
展開図を見てみると線分SPとTRの位置関係は図のようになります.
これは△APS∽△ART∽△AA’C’という関係があり,相似比は辺の比(円周)ではなく,中心角の比を用いると計算が楽になります.
そのため
$$\rm \bigtriangleup APS:\bigtriangleup ART:\bigtriangleup AA’C’\\=AP:AR:A’A’\\=\frac{144°}{360°}:\frac{144°+180°}{360°}:\frac{360°}{360°}$$
上記よりAP:AA’=PS:A’C’,AR:AA’=RT:A’C’となり,A’C’は6cmとなっているので
$$\rm PS=\frac{144°}{360°}\times6[\rm cm], \rm RT=\frac{324°}{360°}\times6[\rm cm]$$
よって
$$(四角形\rm PSTR)=(上底+下底)\times(高さ)\div2\\=(\rm PS+\rm RT)\times PR\div2\\=\frac{156}{5}[\rm cm^2]$$
引用文献
- 都立青山高等学校HP URL: http://www.aoyama-h.metro.tokyo.jp/mokuji14.htm 閲覧日:2016年度8月22日