都立戸山の大問4を解く上でのポイント

• 動点の位置の把握
• 動点とその他の点との位置関係
• 立体の対角線

をしっかり理解しましょう．

都立戸山 数学 2016年度(問題)^*1

〔問１〕1，2分ほどで解けるといいと思います！

【ヒント】

動点Pと点Hの位置関係からどのような直方体が描けるか考えれば簡単に解けます．

【詳しい解説】

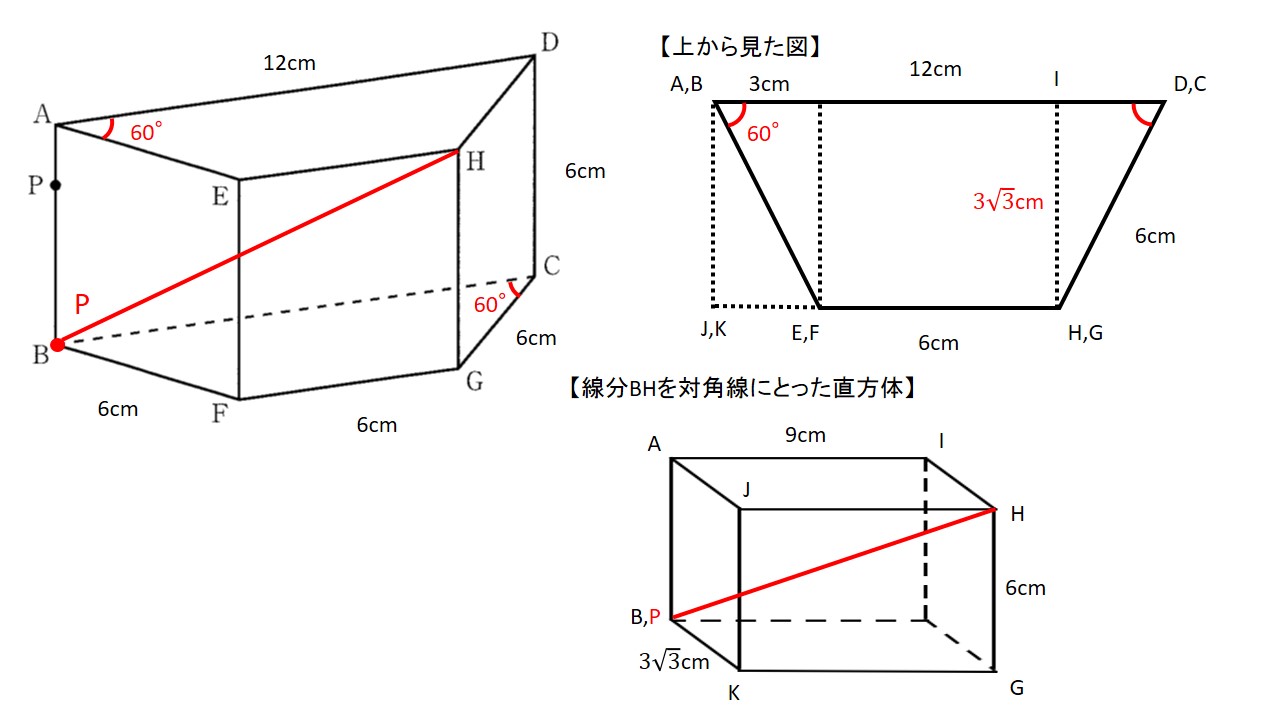
動点Pは3秒後は点Bにいます．

よって線分PH＝線分BHとなります．

∠CBF＝60°より上から見た等脚台形の高さは

$$3\sqrt{3}[\rm cm]$$

よって線分BHを対角線にとった直方体は

$$縦=3\sqrt{3}[\rm cm], 横=9[cm], 高さ=6[cm]$$

ゆえに対角線BHは

$$\rm BH=\sqrt{(3\sqrt{3})^{2}+9^{2}+6^{2}}\\=\sqrt{27+81+36}\\=12[cm]$$

〔問２〕７分程度で解けると試験時には有利！途中式も丁寧に！

【ヒント】

点Pが辺BC上のどの辺りにあるのか考えてみましょう．

【詳しい解説】

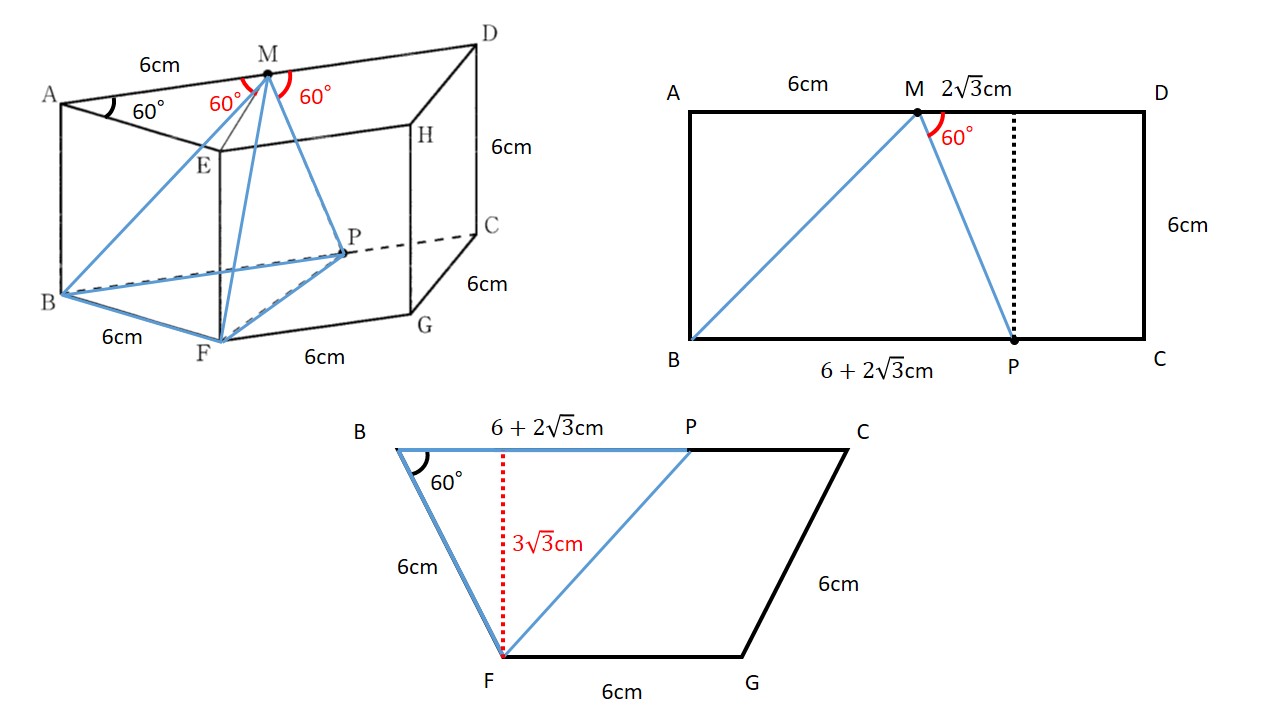
まずは∠AMEの大きさがいくつか考えてみましょう．

点Mが辺ADの中点であることから線分AM＝6cm．

つまり△AMEはAM=AE＝6cmの二等辺三角形となります．

仮定より∠MAE＝60°なので，底角∠AME＝∠AEM＝60°の正三角形になることがわかります．

よって∠DMP＝∠AME＝60°．

動点Pの位置は三平方の定理より

$$\rm BP=AM+CD\times\frac{1}{\sqrt{3}}\\=6+6\times\frac{1}{\sqrt{3}}\\=6+2\sqrt{3}[cm]$$

等脚台形BFGC上にある△BFPを底面としたとき，高さは辺ABになるため6cm．よって三角錐M-BFPの体積は

$$\rm(三角錐M-BFP)=(底面△BFP)\times(高さAB)\times\frac{1}{3}\\=(BP\times(高さ)\times\frac{1}{2})\times AB\times\frac{1}{3}\\=((6+2\sqrt{3})\times3\sqrt{3}\times\frac{1}{2})\times6\times\frac{1}{3}\\=18\sqrt{3}+18[cm^{3}]$$

〔問３〕5分程度で解けるといいでしょう！

【ヒント】

どこまでが６cmなのか，どこからが長さが変わるのか考えてみましょう．

そこから線分PQを対角線にとった直方体を見つけ，もう一度６cmになるところを探す．

【詳しい解説】

まずは上の図までは線分PQは6cmで一定であることがわかります．

つまり動点Pが点M，動点Qが点Eから線分PQは異なる長さになりその後，もう一度６cmになります．

よって動点Pが点Mからt秒後に６cmになるとします．

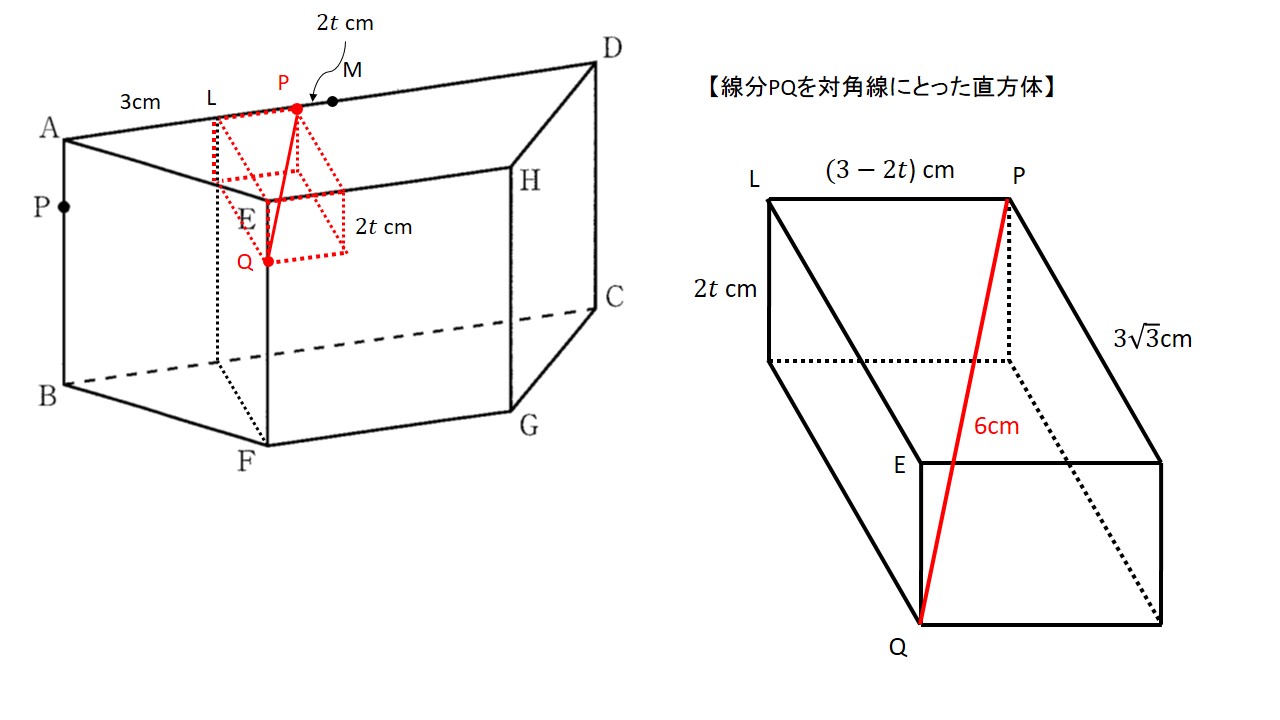
点Eから辺ADに垂直に引いた足を点Lとし，図のような直方体を取ります．

ここで直方体の辺PLの長さが(3-2t)cmになり，$$t>\frac{3}{2}$$のとき辺PLは負の値になりますが，直方体の対角線を求めるときに２乗するため，ここでは気にしないでおきます．

では対角線が6cmになるように方程式を立てます．

$$\rm LE^{2}+EQ^{2}+LP^{2}=PQ^{2}\\(3\sqrt{3})^{2}+(2\it t\rm)^{2}+(3-2\it t\rm)^{2}=6^{2}\\8\it t\rm^{2}-12\it t\rm=0\\\it t\rm(2\it t\rm-3)=0$$

ここでt=0は動点Pが点M，動点Qが点E上にいるときなので

$$t=\frac{3}{2}[秒]$$

ゆえに点Qが点Gを出発してから点Eまでが６秒なので

$$答えは\frac{15}{2}秒後となります．$$

引用文献

1. 都立戸山高等学校HPより
   http://www.toyama-h.metro.tokyo.jp/
   閲覧日：2016年9月10日