中学数学では、算数と違い公式を覚えて計算をラクに速くしていく必要があります。
教科書にはたくさんの公式が書いてあるし、教科書は単元ごとにずらずらと文章と公式が書いてあるだけなので、正直わかりにくいところがあります。
何が大事でどれを優先したらいいのかわからない！結局どれ先に覚えたら良いの？という方向けに数を絞って紹介していきます。
三平方の定理
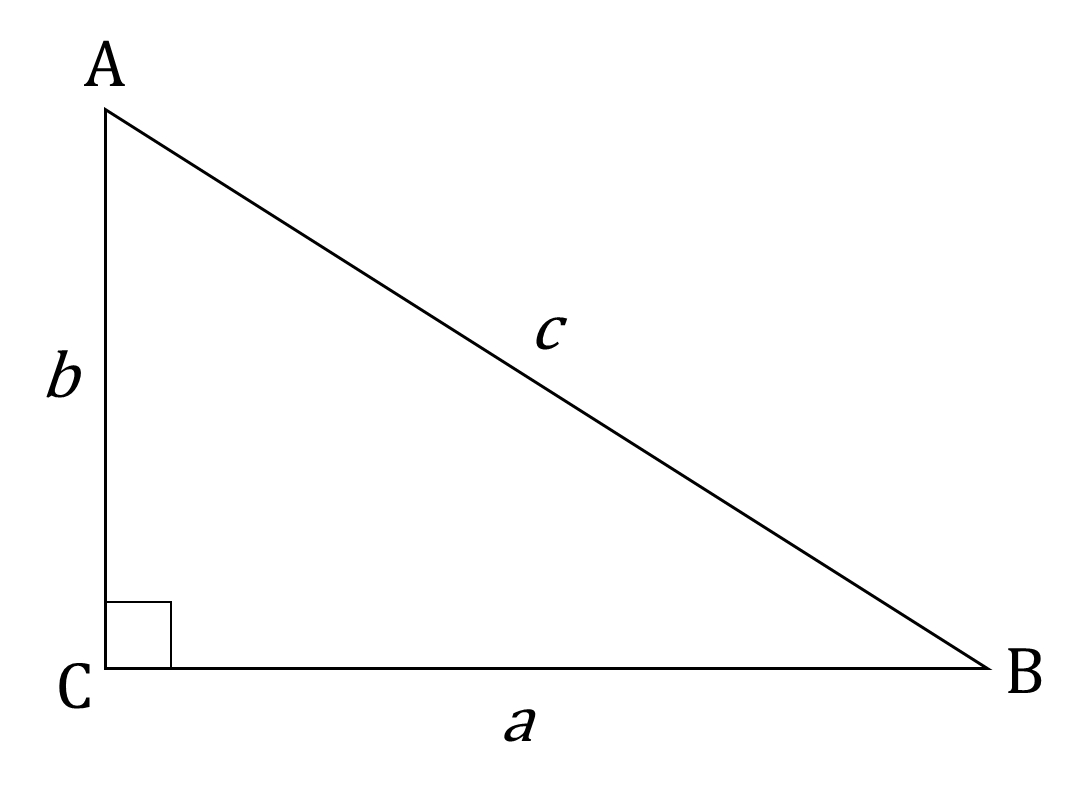
△ABCで、∠C = 90°のとき、
$$\begin{eqnarray*}&&{\Large a^2 +b^2=c^2} \\
\end{eqnarray*}$$
また、その逆も成り立つ。（△ABCで、上の式が成り立つとき、∠C = 90° )
この公式は図形問題ではもちろん、グラフを用いた問題でも大活躍します。
因数分解
下の４つの公式は因数分解の問題を解くためには欠かせません。加えて式を展開するときにも大幅な時間節約になるので、確実に覚えるようにしましょう！
$$\begin{eqnarray*}&& {\Large a^2-b^2=(a+b)(a-b)} \\
&& {\Large a^2+2ab+b^2=(a+b)^2} \\ && { \Large a^2-2ab+b^2=(a-b)^2} \\ &&{ \Large x^2+(a+b)x+ab=(x+a)(x+b)}
\end{eqnarray*}$$
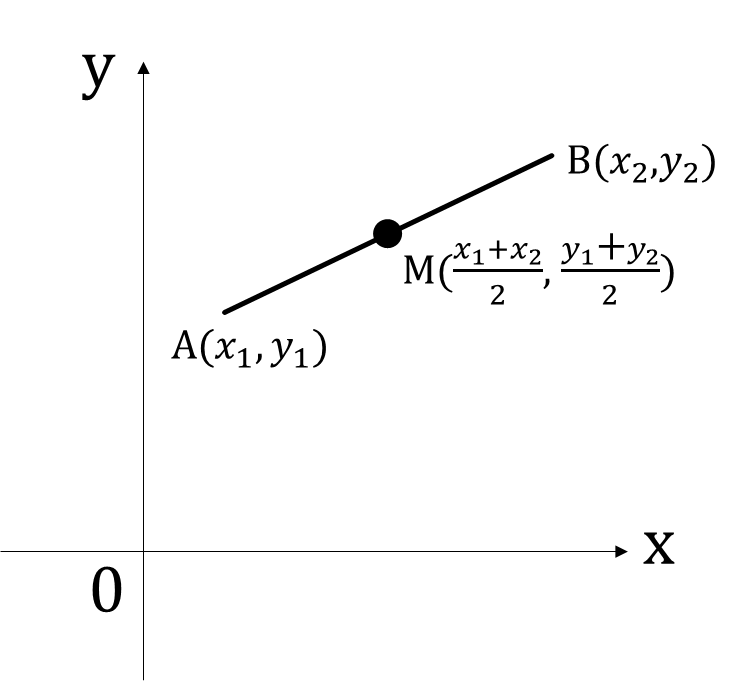
中点の座標
$$\begin{eqnarray*}&&{\Large A(x_1,y_1)、B(x_2,y_2)の中点の座標Mは、M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) }\\
\end{eqnarray*}$$
中点連結定理
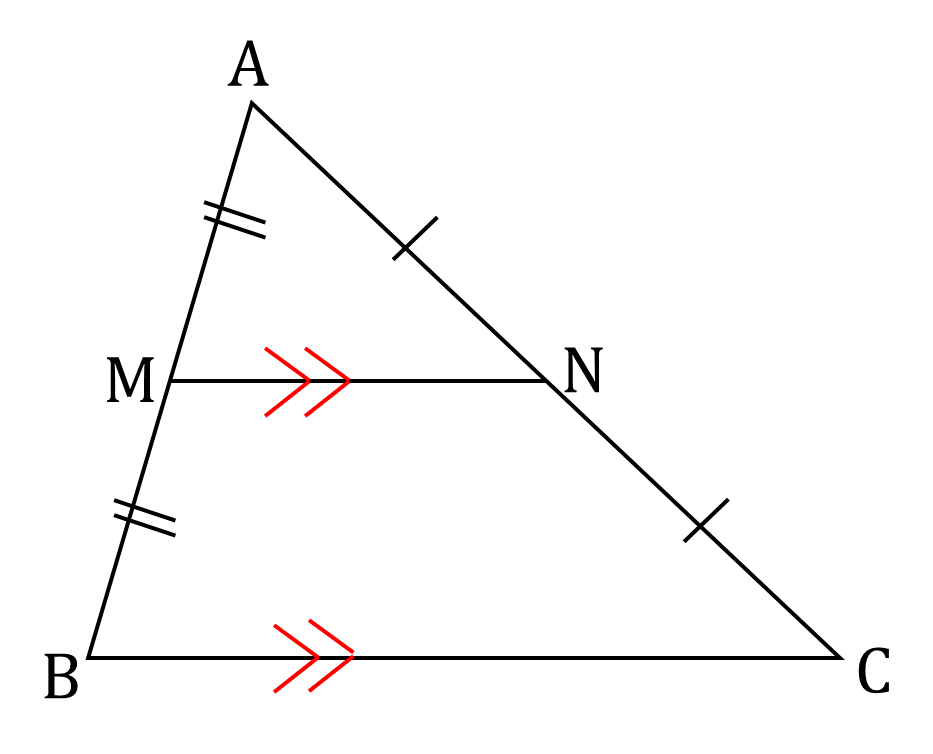△ABCにおいて、AB、ACの中点をそれぞれM、Nとすると次の二つの条件が成り立つ。
&&{\Large MN \parallel BC （線分MNと線分BCは平行）} \\ &&{ \Large MN=\frac{1}{2}BC }\
\end{eqnarray*}$$
三角形の辺の中に二つ中点が出てきたら、とりあえずそれらを補助線で結んでみましょう！
解の公式
$$\begin{eqnarray*}&&{ \Large ax^2+bx+c=0 の解は x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} } \\
\end{eqnarray*}$$
この式を使えばどんな二次方程式も解けるという万能な式です。暗唱できるようになりましょう。
二次方程式の問題を見たときにはじめは因数分解できないか考えることが最優先ですが、因数分解できないor因数分解が思いつかない場合はこの公式を使えば必ず解けます。
角の二等分線の定理
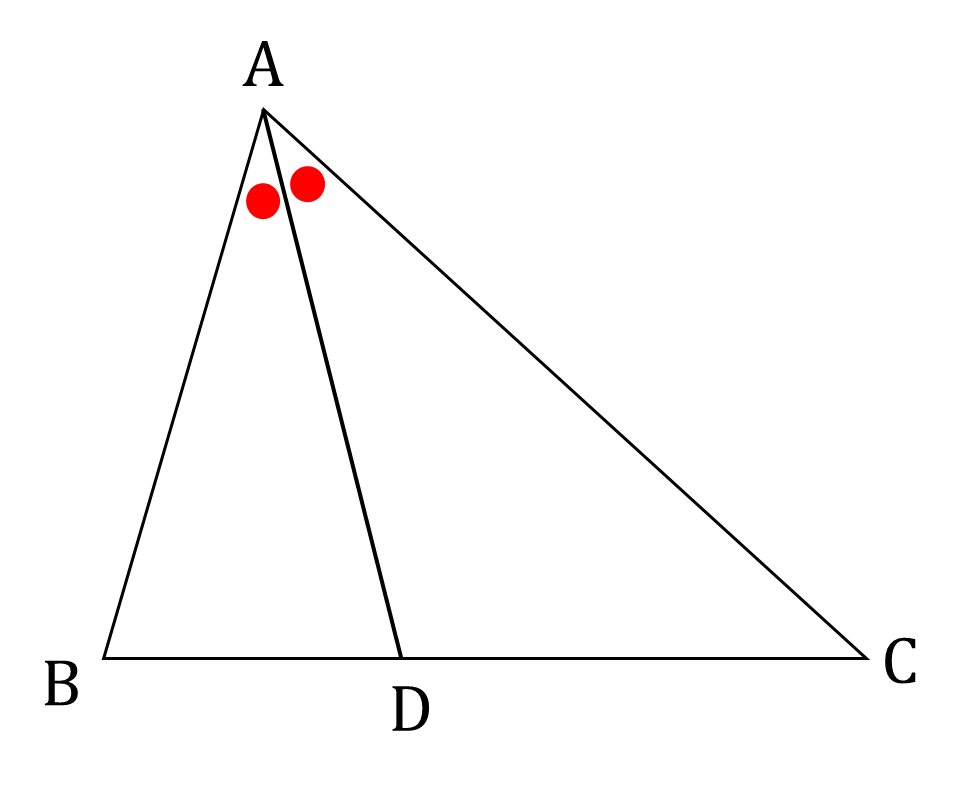
△ABCにおいて$$\begin{eqnarray*}
&&{ \Large \angle BAD=\angle CAD のときAB:AC=BD:DC } \\
\end{eqnarray*}$$
この公式は平面図形の問題を解く際にとても活躍します。「二等分線」というワードが出てきたら、この公式を使うのでは？と思っていいでしょう。
錐体の体積
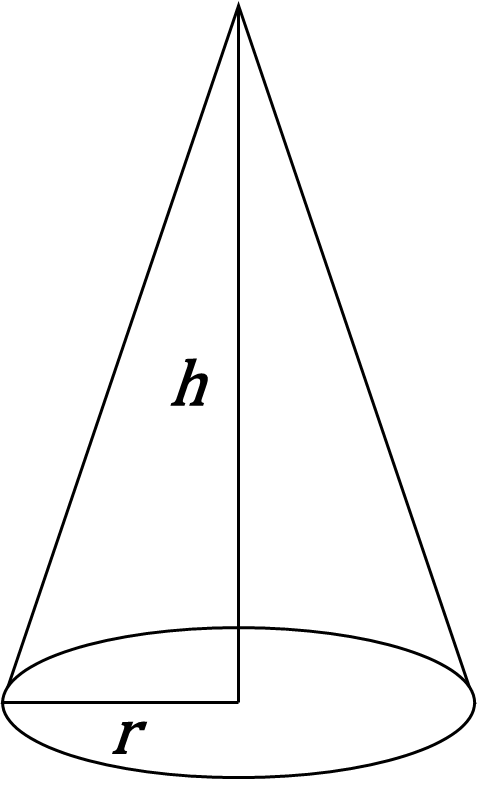
円錐について、底面の円の半径をｒ、高さをｈとすると、その円錐の体積Vは、$$\begin{eqnarray*}
&&{\Large V=\frac{1}{3}\pi r^2 h} \
\end{eqnarray*}$$
1/3を掛けるのを忘れないようにしましょう！
球の公式（表面積、体積）
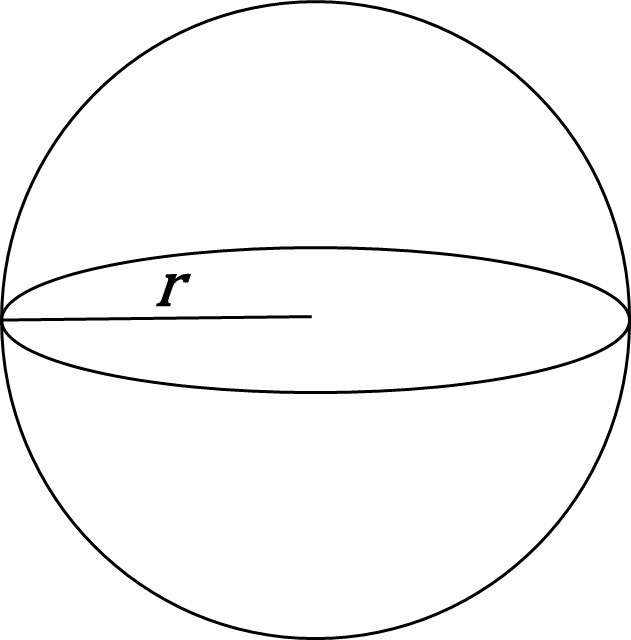
球について、その半径をrとすると、その表面積Sは$$\begin{eqnarray*}
&& {\Large S=4 \pi r^2} \
\end{eqnarray*}$$
その体積Vは$$\begin{eqnarray*}
&&{ \Large V=\frac{4}{3} \pi r^3} \
\end{eqnarray*}$$
表面積は「心配ある事情、心（４）配（π）ある（r）事情（２乗）」、体積は「身の上に心配あるから参上、身（３）の上に心（４）配（π）ある（r）から参上（３乗）」で覚えましょう！
おうぎ形の面積
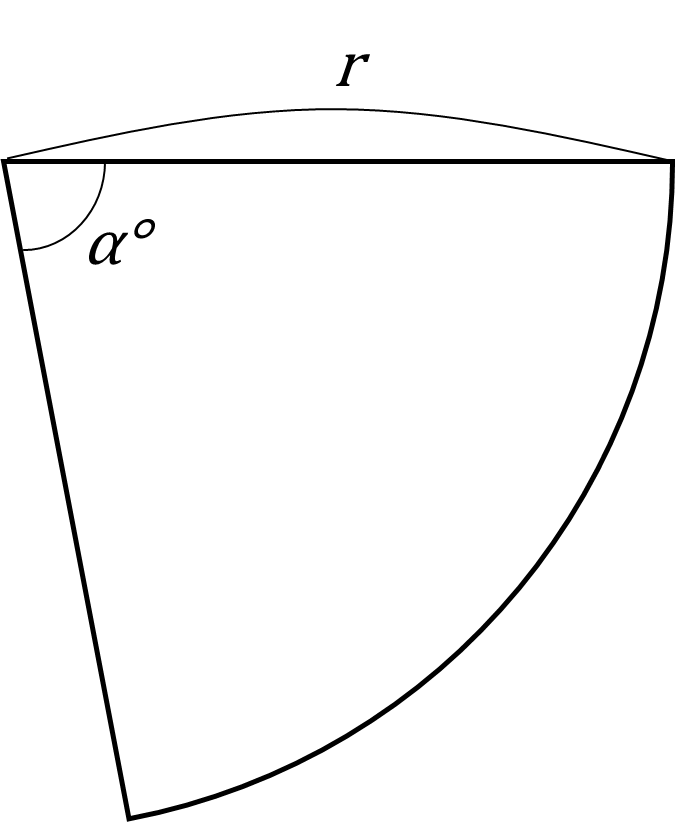
半径の長さr、中心角α°のおうぎ形の面積Sは、$$\begin{eqnarray*}
&& { \Large S=\pi r^2 \times \frac{α}{360} } \
\end{eqnarray*}$$
この式で、「π×rの2乗」の部分はご存知、半径rの円の面積を表しますよね。おうぎ形は円の一部であり、中心角α°のおうぎ形は円（＝中心角360°）の360分のαの部分と考えることができます。その後ろにかけているα/360はそのことを意味しています。
また面積の公式にはもう一つあります。これも覚えておくと便利でしょう。
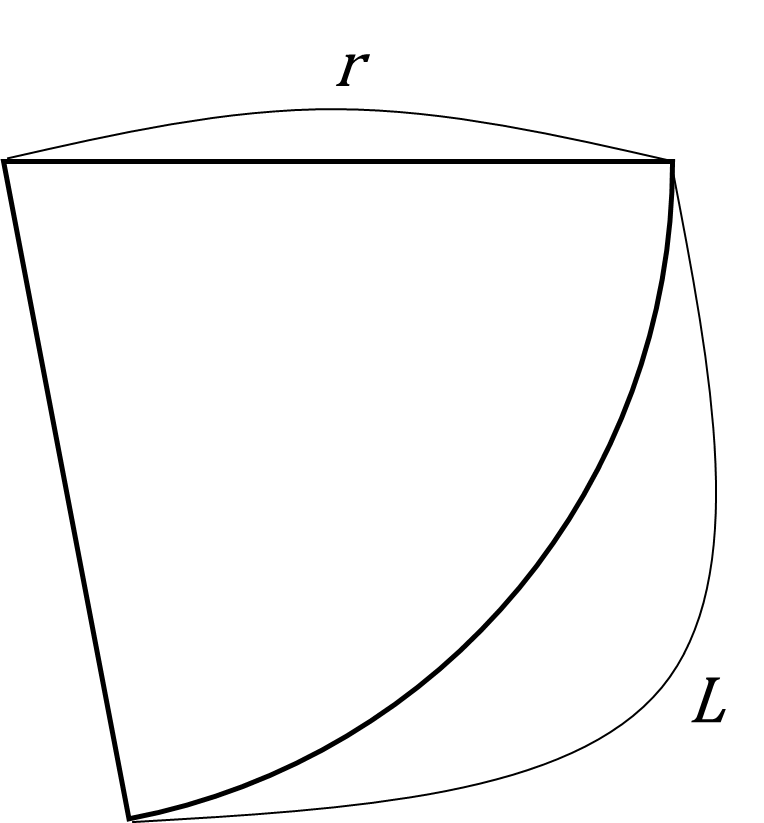
半径の長さr、弧の長さLのおうぎ形の面積Sは、$$\begin{eqnarray*}
&& {\Large S=\frac{1}{2} rL}\
\end{eqnarray*}$$
この公式はおうぎ形の中心角が与えられてないときに役立ちます。この長さLは、おうぎ形の中心をα°とすると、$$\begin{eqnarray*}
&&L=2 \pi r \times \frac{α}{360} \
\end{eqnarray*}$$ なので、これを代入すると一つ目の公式が導けます。
円周角の定理
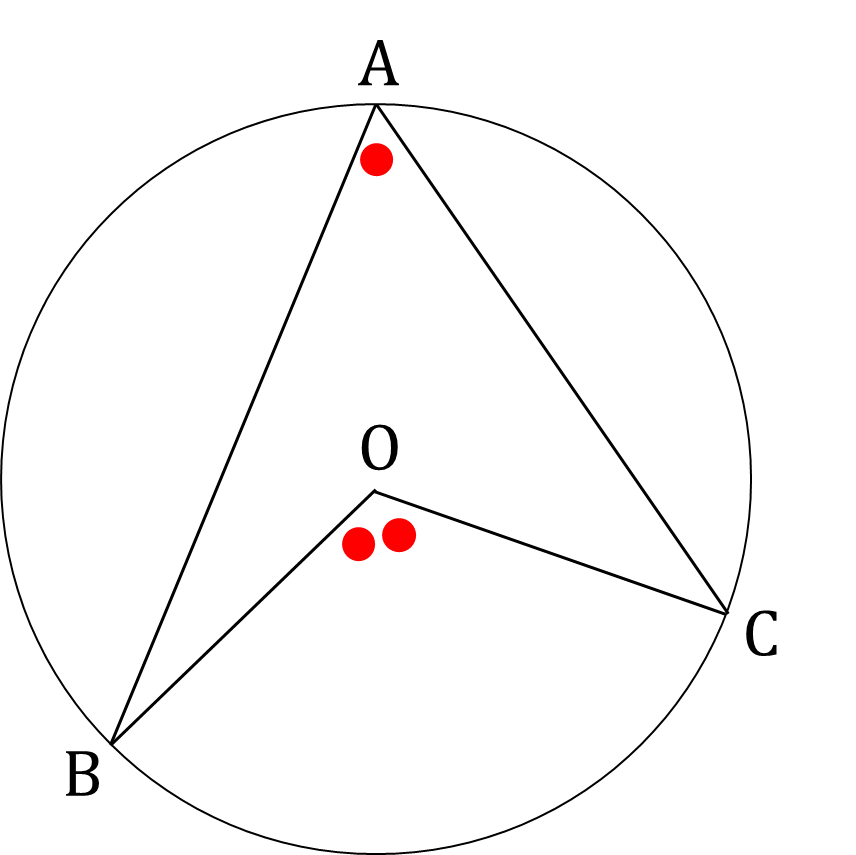
点Oを中心とする円の円周上に上図のように点A、B、Cをとると、下の式が成り立つ。$$\begin{eqnarray*}
&&{\Large \angle BAC= \frac {1}{2} \angle BOC }\
\end{eqnarray*}$$
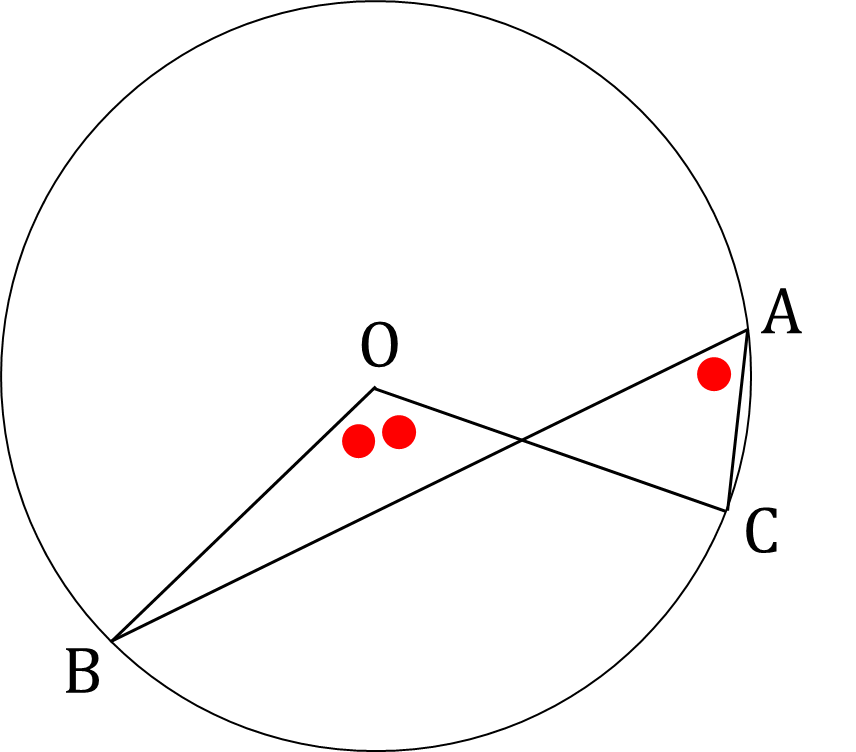
これを円周角の定理と言います。もちろん下のように点があっても円周角の定理は成り立ちます。
円の中で角度を求める問題では必ず使うといってもいいでしょう。
公式は数学の問題を解いていくうえで大変重要なものです。上にあげた１０の公式を確実に頭に入れて使いこなせるようにしておきましょう！
