【都立西高等学校】2016年度数学過去問大問4解説

都立西の大問4を解く上でのポイント

• 動点の動きと位置
• 図形の相似と面積比，体積比

が重要です．

都立西 数学 2016年度(問題)^*1

〔問１〕1，2分で終わらせましょう！

【詳しい解説】

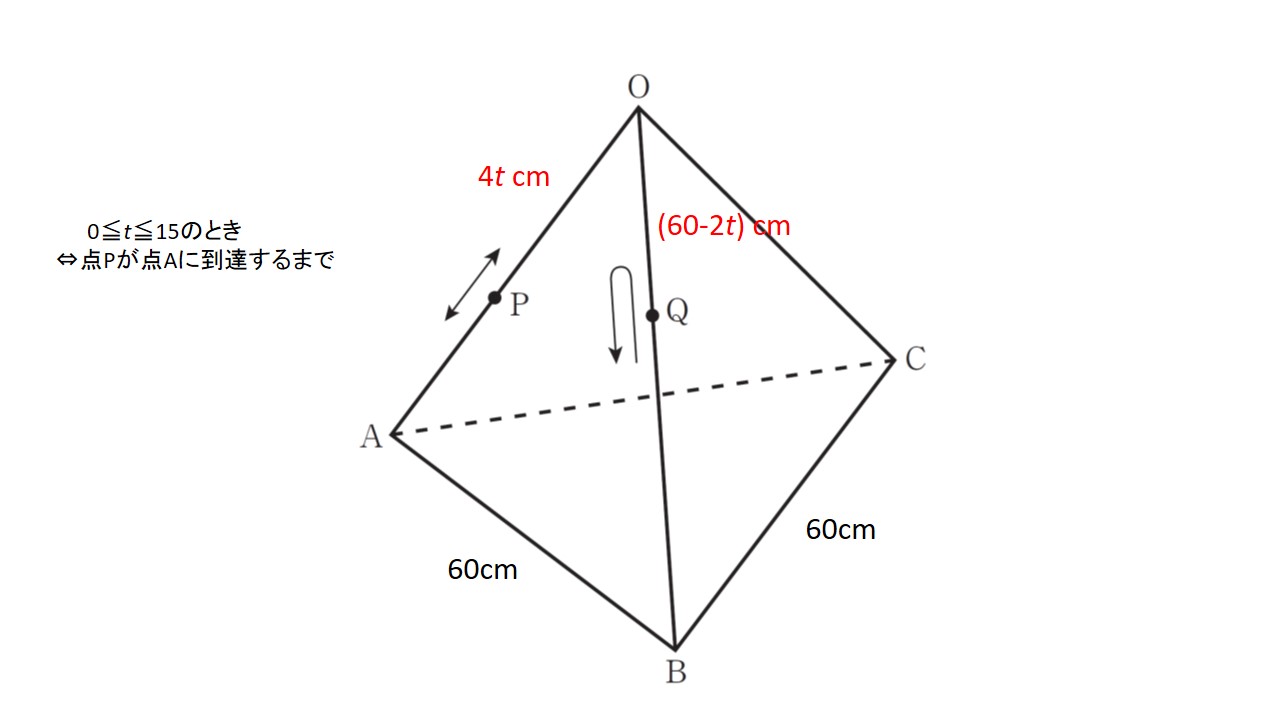
図のようにOP＝2OQになるまでの時間をt［秒］とおくと

$$\rm OP=4\it t\rm [cm], OQ=60-2\it t\rm [cm]$$

よってOP＝2OQに代入すると

$$4t=2\times(60-2t)\\8t=120\\t=15[秒]$$

〔問２〕（１）5分程度と解けると良い！途中式も丁寧に！

【ヒント】

体積をむやみやたらに求めるのではなく，底面の相似を利用してあげると簡単に求まります．

【詳しい解説】

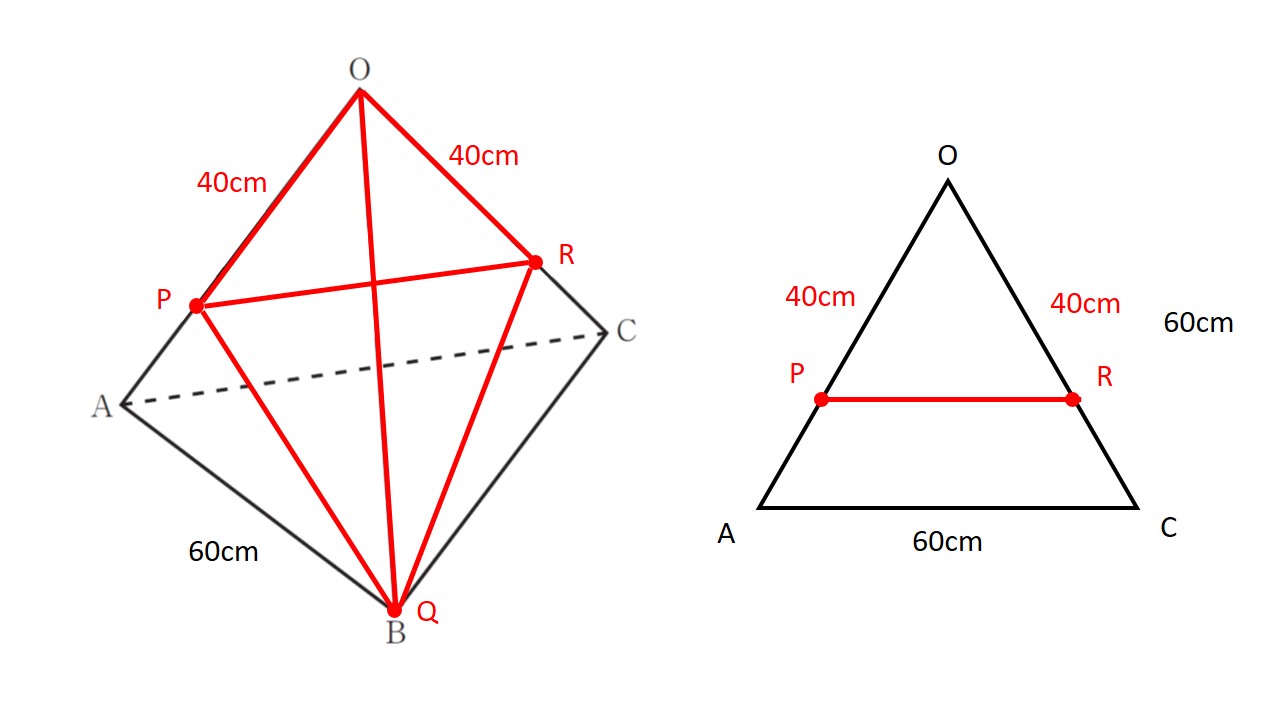
仮定よりx=80，点Rの速さは毎秒1cmであることからOP＝OR＝40cmとなります．

これを利用して立体O-PQRの底面を△OPRにすることで，立体O-PQRと立体O-ABCの体積は高さが共通であることから底面積のみで変化することがわかります．

よって底面積の比を求めます．

$$\rm △OAC∽△OPRより相似比は\\△OAC:△OPR＝60:40=3:2\\面積比は△OAC:△OPR＝9:4\\\frac{△OPR}{△OAC}=\frac{4}{9}$$

ゆえに

$$\rm(立体O-PQR)=\frac{4}{9}(立体O-ABC)$$

したがって答えは

$$\frac{4}{9}倍$$

〔問２〕（２）5分程度と解けると良い！

【ヒント】

点Rの動きはまず無視し，OP=OQになるときを考えてみましょう．

そのときに動点Pと動点Qの動きを整理すると良いでしょう！

【詳しい解説】

ヒントにあるように，まず動点Pと動点Qの動きと位置について考えます．

30<x <60を細かく分割し，位置関係を確認しましょう．

(i) 30<x ≦40のとき

動点PはOP＝0～40 cm
動点QはOQ＝0 cm（点Oから動かない）

(ii) 40<x ≦45のとき

動点PはOP＝40～60 cm
動点QはOQ＝0～10 cm

(iii) 45<x <60のとき

動点PはOP＝60～0 cm
動点QはOQ＝10～40 cm

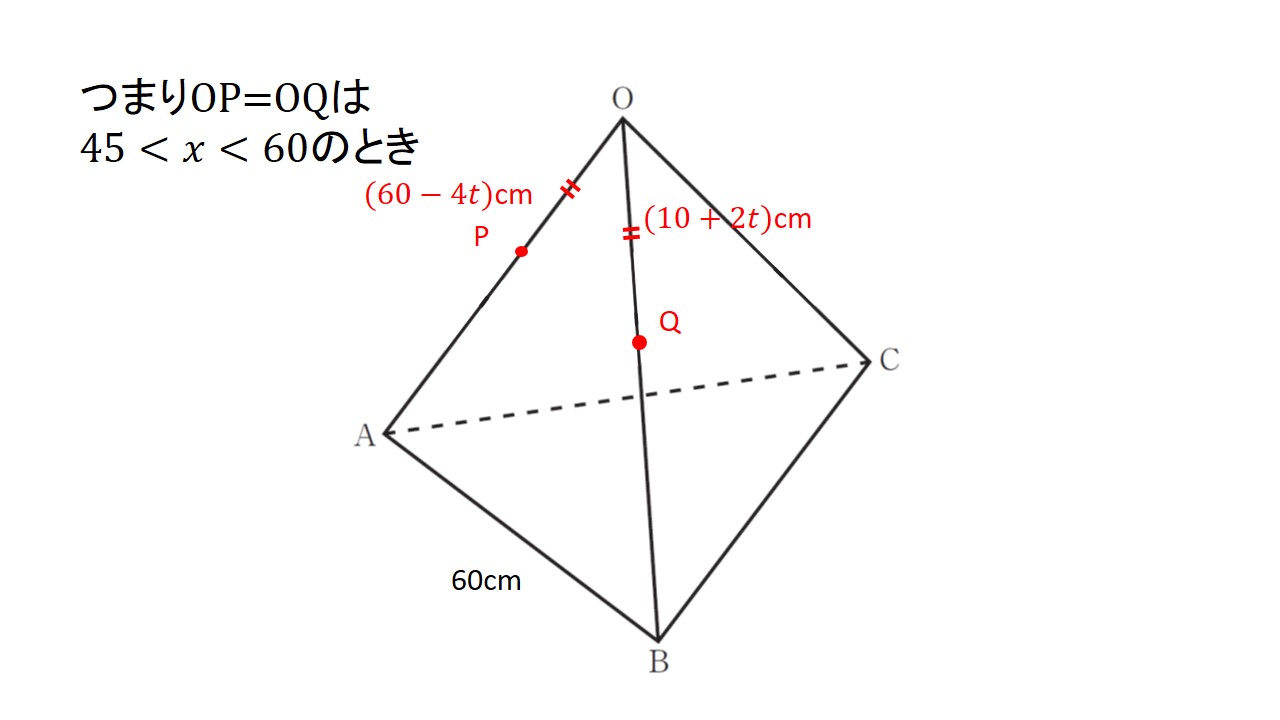
このことから，OP=OQとなるタイミングがあるのは(iii)の 45<x <60のときです．

ではx＝45[秒]からt 秒後にOP=OQとなることを式に表し，解くと

$$\rm OP=OQ\\60-4\it t\rm=10+2\it t\rm\\6\it t\rm=50\\\it t\rm=\frac{25}{3}[秒]$$

このときの線分OP（または線分OQ）の長さは

$$10+\frac{25}{3}\times2=\frac{80}{3}[\rm cm]$$

ここで仮定より動点Rは1往復するのに2分以上かかる．つまり片道1分以上かかることがわかります．
a <1 [cm/s]が条件となります．

$$\rm 動点Rは45+\it t\rm [秒]後に\\線分ORが\frac{80}{3}[cm]になることから\\\it a\rm(45+\frac{25}{3})=\frac{80}{3}\\\it a\rm(\frac{160}{3})=\frac{80}{3}\\\it a\rm=\frac{1}{2}[cm/s]$$

よって

$$a\rm=\frac{1}{2}[cm/s]$$

引用文献

1. 都立西高等学校HP　URL: http://www.nishi-h.metro.tokyo.jp/menu09.html
   閲覧日:2016年9月7日