前回(比例を表す式)解答
//////////////////////////////////////////////////
ここに「比例を表す式」のURLを貼る
//////////////////////////////////////////////////
(1)
$$y=2\times3x=6x$$
よってyはxに比例し、比例定数は6となる。
(2)
$$y=100\times x=100x$$
よってyはxに比例し、比例定数は100となる。
(3)
$$y=ax$$
に代入すると
$$\begin{eqnarray*}
15&=&a\times10\\
a&=&\frac{15}{10}\\
a&=&\frac{3}{2}
\end{eqnarray*}$$
より比例定数は求まった。比例の式は以下のとおりである。
$$y=\frac{3}{2}x$$
となる。またx=4のとき、yの値は
$$\begin{eqnarray*}
y&=&\frac{3}{2}\times4\\
y&=&\frac{3\times4}{2}\\
y&=&6
\end{eqnarray*}$$
よりy=6となった。y=9のとき、xの値は
$$\begin{eqnarray*}
9&=&\frac{3}{2}x\\
x&=&9\times\frac{2}{3}\\
x&=&\frac{9\times2}{3}\\
x&=&6
\end{eqnarray*}$$
よりx=6となった。
(4)
$$y=x\times x=x^{2}$$
よってyはx2に比例し、yはxに比例していない。
(5)
$$y=24-x$$
よってyはxに比例していない。(y=axの関係が成り立っていないため)
比例の式をグラフに
ではこれから比例の式を座標平面上に表してみましょう!
「座標平面って何?」という方は下のブログで!
////////////////////////////////////////////
「座標平面について」の
URLをここに貼る
/////////////////////////////////////////////
では前回の演習問題(3)の問題を用いて表とグラフを書きましょう。
比例の式は
$$y=\frac{3}{2}x$$
であるので、下の表を完成させましょう。
| x座標 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y座標 |
| x座標 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y座標 | -6 | $$-\frac{9}{2}$$ | -3 | $$-\frac{3}{2}$$ | 0 | $$\frac{3}{2}$$ | 3 | $$\frac{9}{2}$$ | 6 |
では上記の表を座標平面上にプロットしましょう。
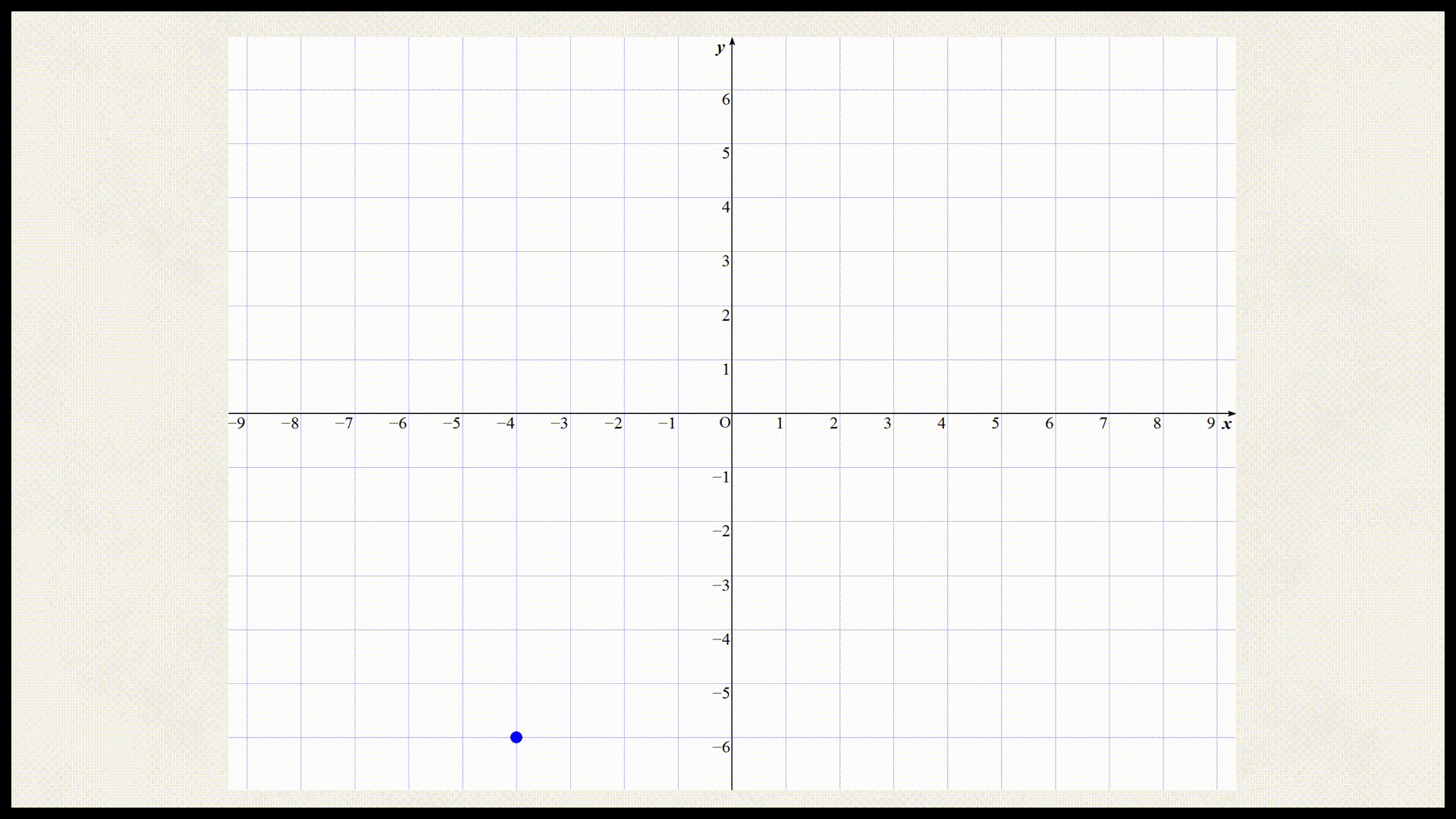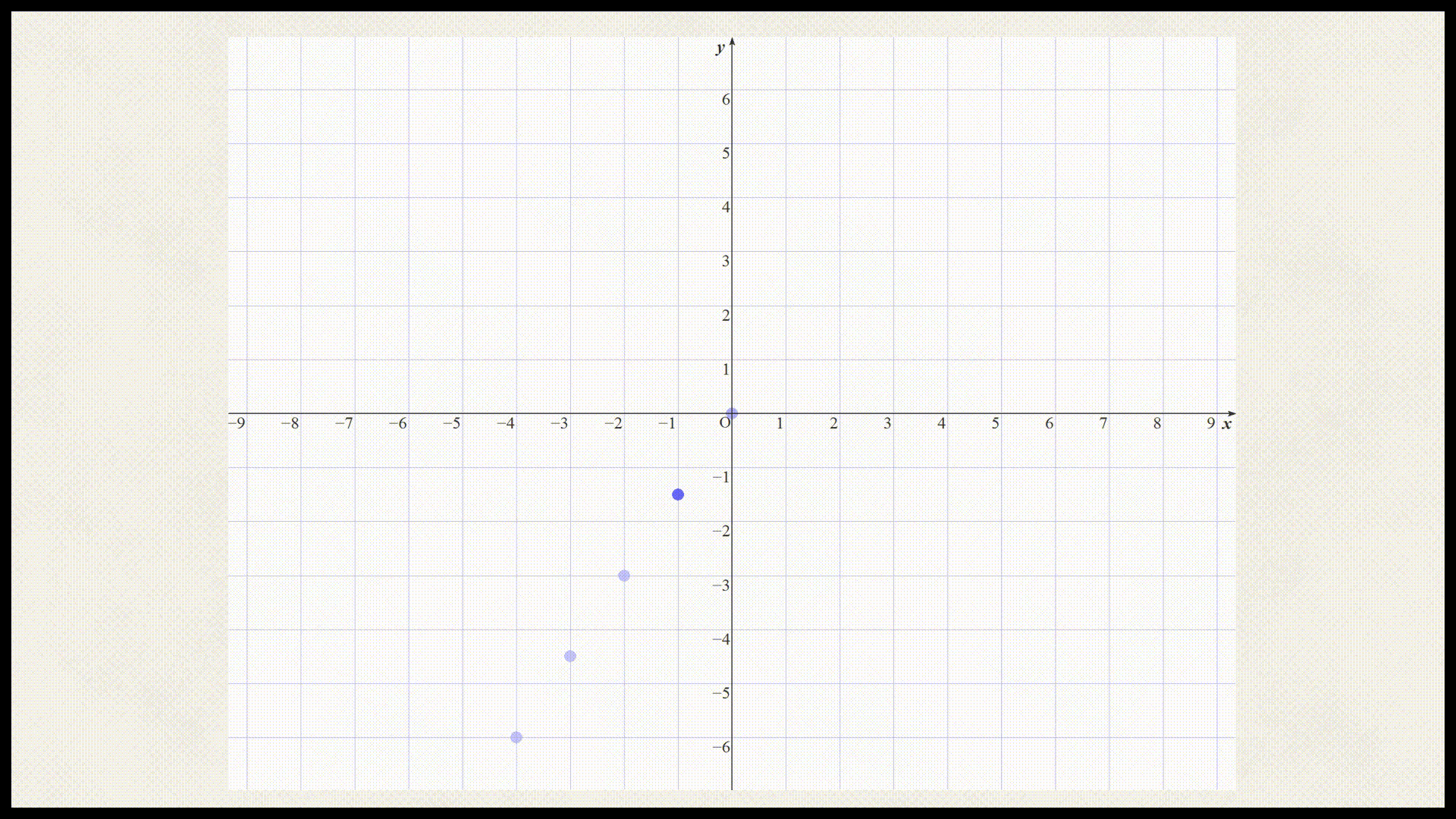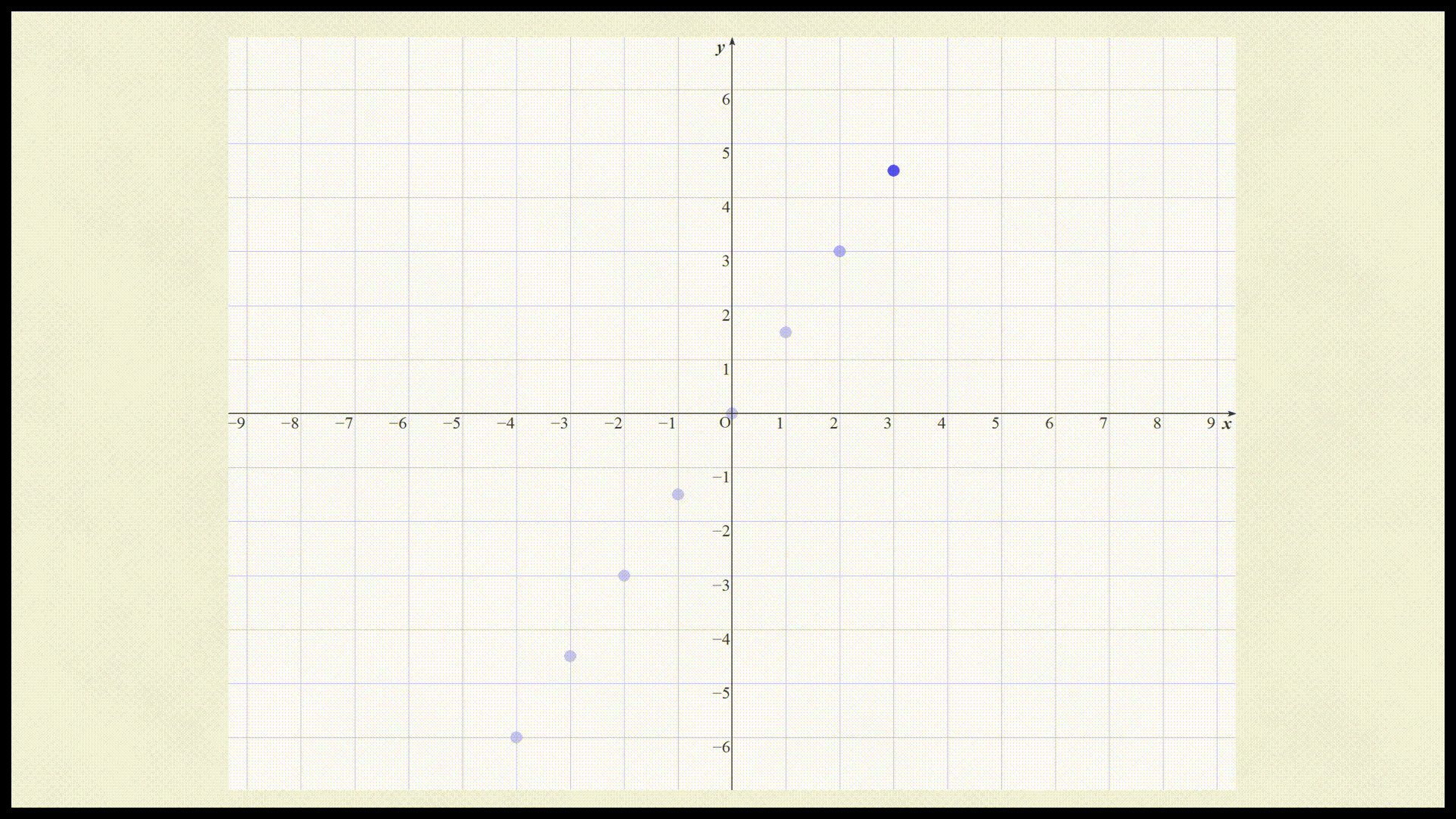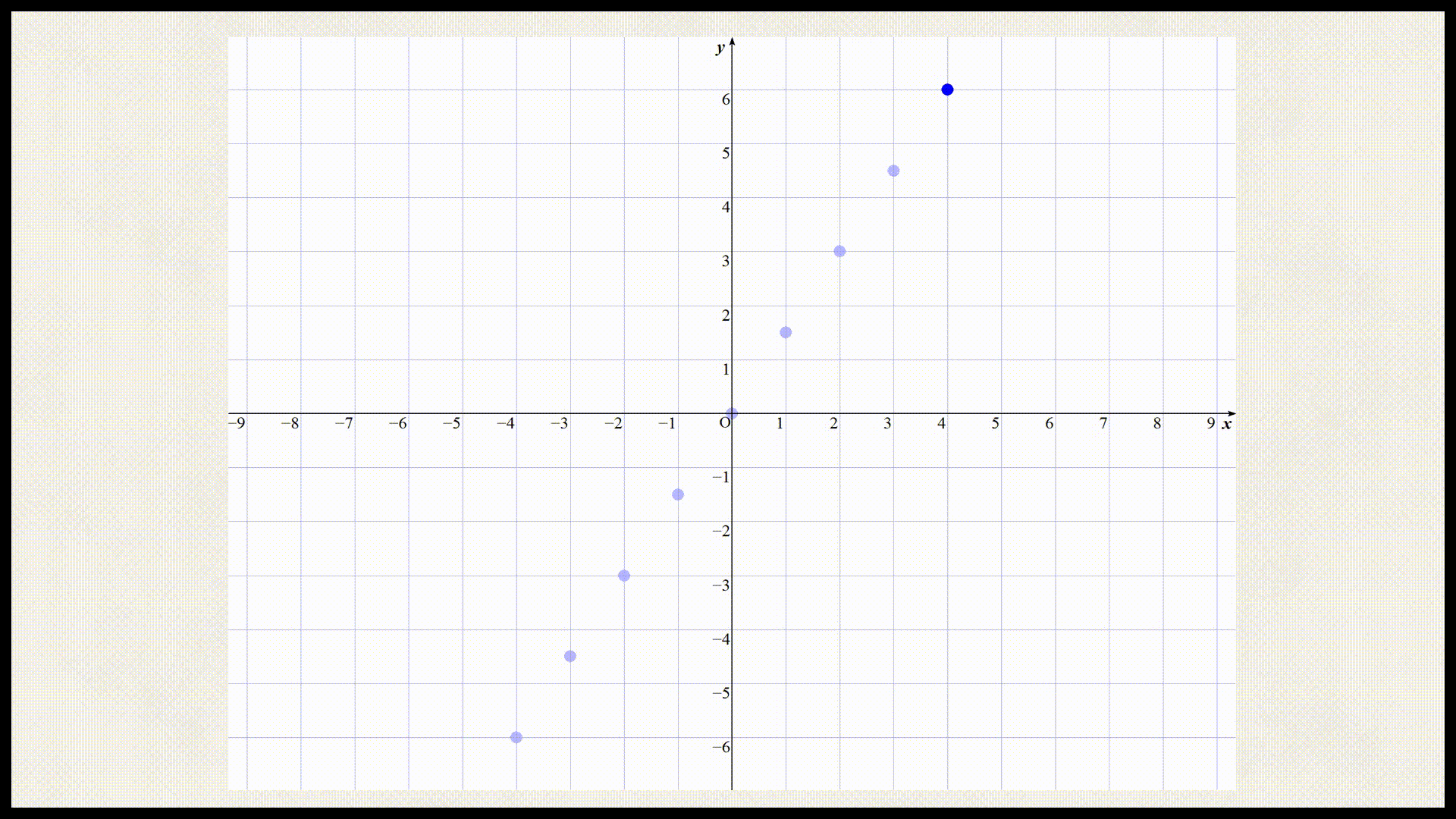
これらの点を直線で結ぶと以下のようになる。
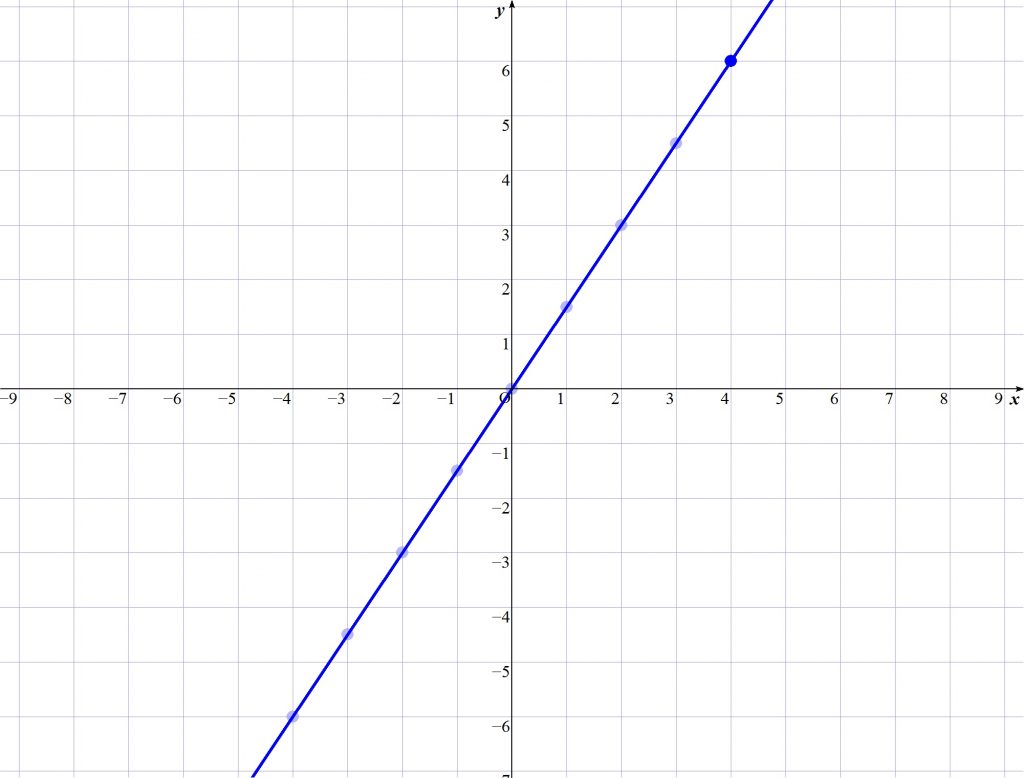
上記が比例におけるグラフになります。
ではグラフの書き方が分かったと思いますので、演習問題をやってみましょう。
次回は比例のグラフをもっと詳しく見ていきます。
演習問題
$$y=-2x$$
のグラフを描いてください。
解答は次のブログで!
//////////////////////////////////////////////////
ここに「比例のグラフ(その2)」のURLを貼る
//////////////////////////////////////////////////
