数学の中で特に苦手な人が多いのが図形問題だと思います。「図形ってひらめきが全てじゃないの？」と思っている人が沢山いる気がします。
しかし、実は図形問題も工夫次第で全くひらめきに頼ることなく問題を解いていくことができます。図形問題でも、他の計算問題と同じで「やること」や「やることの順序」が決まっているのです。
ひらめきで解いてるいるように見える人も(一部を除いて)、実は解くときに決まったことを決まった順序で素早くやっているだけなのです。
Contents
図形を丁寧に描いて、条件を書き込む
図形問題では、問題用紙に図形が描いてあることがありますが、図が小さかったり文章しかなくて図がなかったりすることがあります。そういうときは定規を使わず、大きく丁寧に描きましょう。そうすることで、見やすくなり図形の性質に気付きやすくなります。
定規を使わないと初めのうちはきれいな円や直線を描くのが難しいかもしれません。しかし、それもフリーハンドで描いてるうちにきれいに描けるようになるものです。
第一、試験などでは定規持ち込み禁止の場合が多くあります。定規がないために、試験で丁寧に図が描くことができなければ意味がないですよね。
図形問題が出来ない生徒を見ていると原因の一番は「描いた図形が汚い」。これな気がします（笑）。
問題の通りに図形が描けているか確認
問題通りに図が描いてないとほとんどの場合、致命傷になります。解き方は全部合ってるのに、点の位置を取り間違えて0点…なんてことはかなり悔しいですよね。
それは本当にもったいない。図を一通り描いたら、間違いがないか必ず確認しましょう。
問題文の情報にチェックを入れていくのがおすすめです。
こんな問題があったら…
読みながら、この赤丸のように情報に印を入れていきます。ちゃんと問題通り図が描けているか確認する際に、その印をつけた部分を重点的に確認すればよいわけです。
印を入れることで、情報の読み落としを発見したり、何を使って解いていくのかを予測するのにも役立ちます。
図形問題に限らず、数学のすべての問題で問題文にチェックを入れていく癖をつけるといいでしょう。
平行や直角を見つける
「平行」「直角」は問題を解いていくうえでカギとなります。問題文に与えられていることが多いですが、自分で見つけないといけないような問題もあります。
以下にどのような場合によく「隠れた平行」「隠れた直角」が出てくるか書いておきます。
隠れた平行
「隠れた平行」は「錯角が等しいとき」「同位角が等しいとき」にあります。「平行な直線の錯角、同位角は等しい」は重要な性質ですが、もちろんその逆、すなわち「二つの直線の錯角、同位角が等しいとき、その二直線は平行」が成り立ちます。
等しい角が２つ出てきたときに、それらが錯角や同位角の位置にないか確認してみましょう。
隠れた直角
「隠れた直角」は「円の中心を通る線が引かれているとき」にあります。これはつまり、円周角の定理より「弦が円の中心を通るとき、その円周角は直角になる」という性質を使ったものです。
これは結構見落としがちです。注意！ちなみに中学数学に限らず、高校数学でもたまに出てきますね。
簡単な例ですが、次のような問題です。
このｘを求めるためには∠ACB＝90°（直角）に気付かなければ解くことはできません。確かに円の中心を通る線（線分AB）が引かれてますね。
ちなみに解答は、∠DAB＝∠DCB＝65°、∠ACB＝90°よりｘ＝∠ACD＝∠ACB－∠DCB＝90°－65°＝25°となります。
証明問題を解くコツ４つ
◎以前に証明問題についての記事を書いているので、まずそちらをご覧ください。↓クリック！！
【数学】中学証明問題を解く4つのポイント
このページでは要点だけをまとめておこうと思います。
1.とにかく図形の性質や条件を覚える
- 三角形の合同条件
- 三角形の相似条件
- 平行線の性質
- 平行四辺形になる条件
- 直角三角形の合同条件
- 二等辺三角形の性質
など
これらは教科書に載っている条件です。これらを覚えないとまず証明問題は解けません。つまり図形の性質の条件を覚えることは最優先事項です。お経のように唱えられるようになるまで、完璧に暗記しましょう！
2.「仮定」と「結論」をチェック、仮定を図に書き込む
上にも書いた通り、問題文を読み進めながら、問題文に出てくる情報にはチェックを入れていきましょう。特に証明問題ではこの作業がとても重要になります。
というのも、証明を書いていくのに一生懸命になるあまり、「結局何が言いたいのか」「どの条件が使えるのか」ということを忘れてしまう人が多いからです。
また証明問題ではたくさんの情報が与えられることが多いです。それらの情報を一目で分かるようにするためにも図に書き込んでいくことは欠かせません。
3.結論を見て、覚えた図形の条件のどれを使うかはじめに決める
証明を書き出す前に、はじめに結論を見て、使う図形の条件を決めることは、証明をスムーズに書いていくためには大切です。
例えば、三角形の合同証明問題で、結論を見てみると、『どうも「二辺とその間の角がそれぞれ等しい」を使いそうだ』と予測が立ったとします。
すると、その条件を使うために、証明しようとする２つの三角形において「２辺の長さがそれぞれ等しい」ことと「その間の角が等しい」ことを、どうにかして示せればよいわけです。
このように数学の問題では、証明問題に限らず、結論から逆算して解答の方針を立てていくという発想が大事です。
4.アルファベットが対応しているか確認する
角度が等しいことを証明に書いていくとき、そのアルファベットの並び方は、証明する図形の点の並び方と同じである必要があります。これはルールなので、守らなければ減点されます。
例えば下の問題で具体的に見てみましょう。
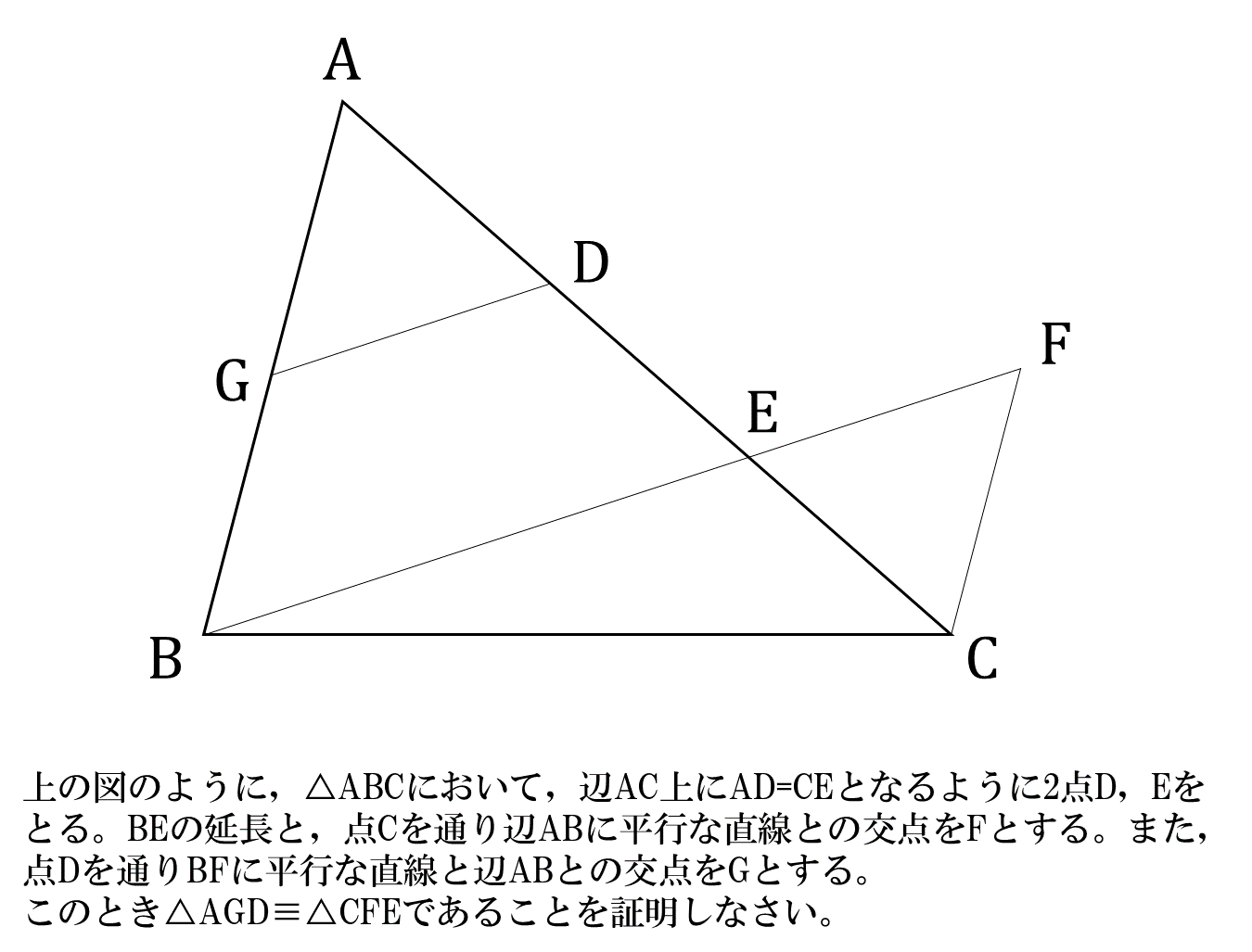
この問題で、△AGD≡△CFEを示すため、錯角∠GADと∠FCEが等しいと証明に書きたいとします。このとき下のように考えて…
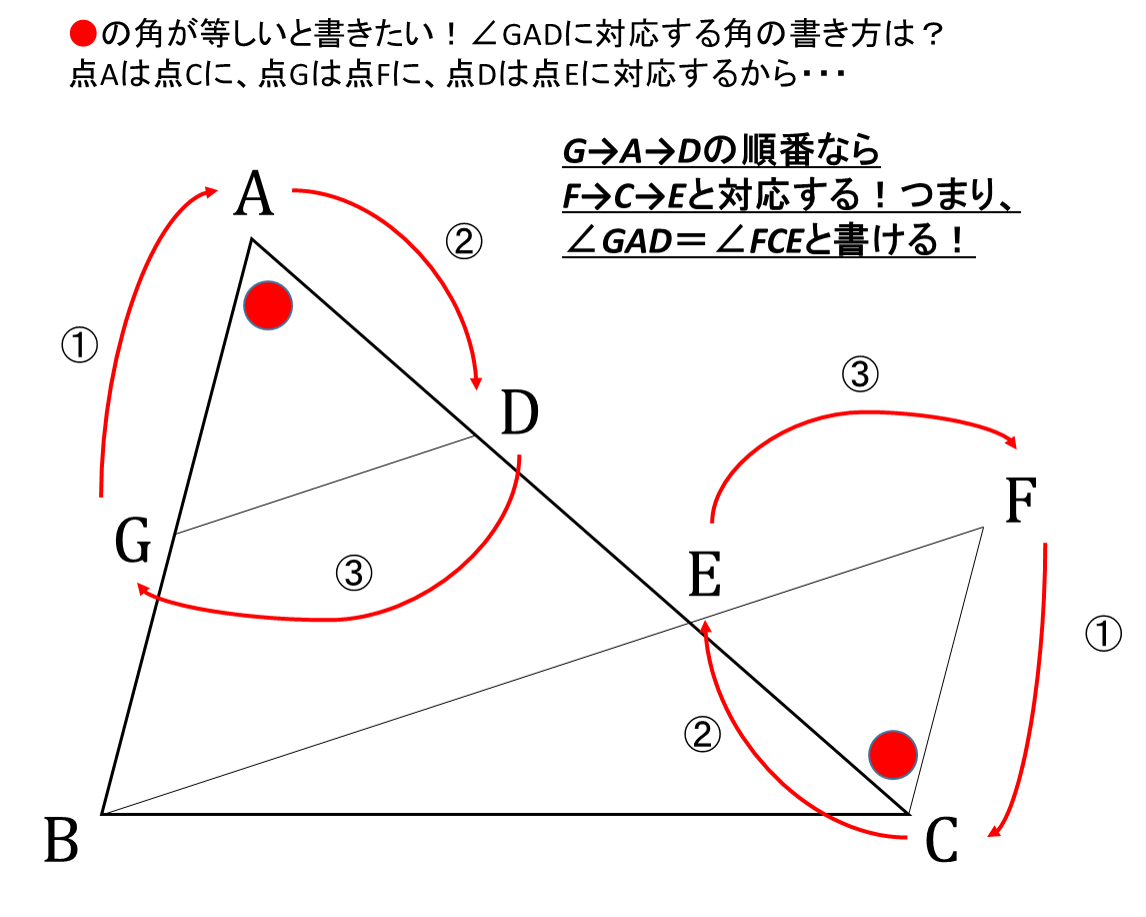すなわち、∠GAD＝∠FCEと書かなければいけません。
∠GAD＝∠ECFは内容的にはなんら問題ないのですが、証明問題となると誤りになります。内容は正しいのに減点食らうなんてもったいないですよね。しっかり見直しをするようにしましょう！
まとめ
いかがでしょうか？上に書いた7点をしっかり定着させれば、図形問題は解けるようになるはずです。はじめのうちは「7つもあるのか…」と思うかもしれませんが、７つのポイントを意識して問題を解いていくうちに、しだいに無意識に使えるようになります。
