【数学】確率を極めるには「場合の数」を極めろ！

「確率は難しいなあ～…」「全然解けない！」「書きだしちゃダメなの？」

確率を苦手とする中学生の口からよく耳にする言葉です．

確率はしっかり理解すればとても簡単です！もちろんそれまでは苦労しなくてはなりません．

みんなできないからこそ，受験では確率ができる・できないで差が広がります！

では確率についてしっかり学んでいきましょう！

「確率」と「場合の数」はとても似ている！

学校でも塾でも，確率を習う前には必ず場合の数を教わります．

このことから場合の数と確率は非常に似ていることがわかります．

そのため確率を極めたければ，場合の数を極めるべし！

では場合の数について見ていきましょう．

場合の数はどうやって求めるの？

条件に合うものを書きだすのも1つの手です！（ただし，せいぜい20個書き出すのが限界なのではないでしょうか？）

書き出すときは「樹形図」または「書き出す」の2種類がありますが，後者の「書き出す」をオススメします．このときに気をつけて欲しいことは辞書順またはアルファベット順に書き出すことが大事です！このようにルールを決めておくことで見落としが少なくなります．

「樹形図」を描くと文字が小さくなり，ゴチャゴチャしてしまい見落とすことも考えられるため，おすすめはしません．

しかし，問題が発展的になればなるほど，場合の数は数百通り，数千通りと数が莫大になっていきます．そうなると書き出すのも…(笑)

では書き出すこと以外にどのようにして場合の数を求めるのか？

場合の数の問題は大まかに分けると順列と組み合わせがあり，これらは掛け算と割り算を駆使することで求めることができます．

では実際に解いてみましょう！

【1】A，B，Cの3人を1列に並べる方法は何通りあるか．^*1

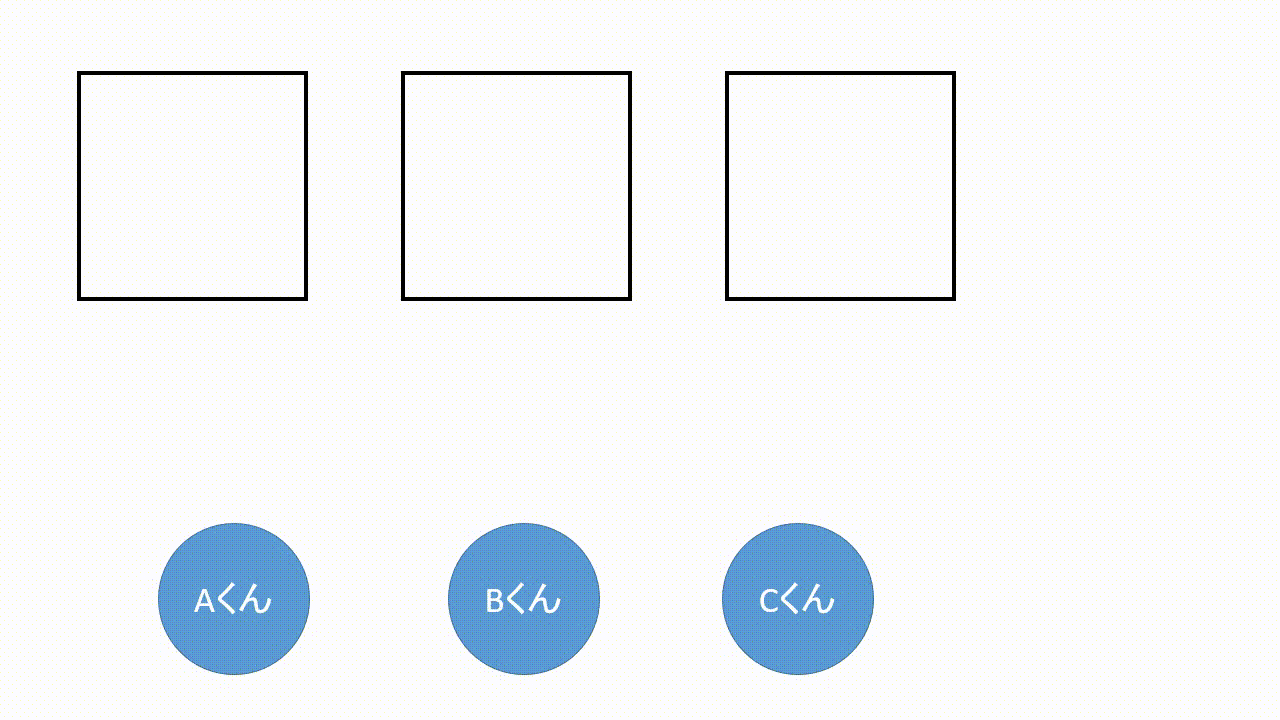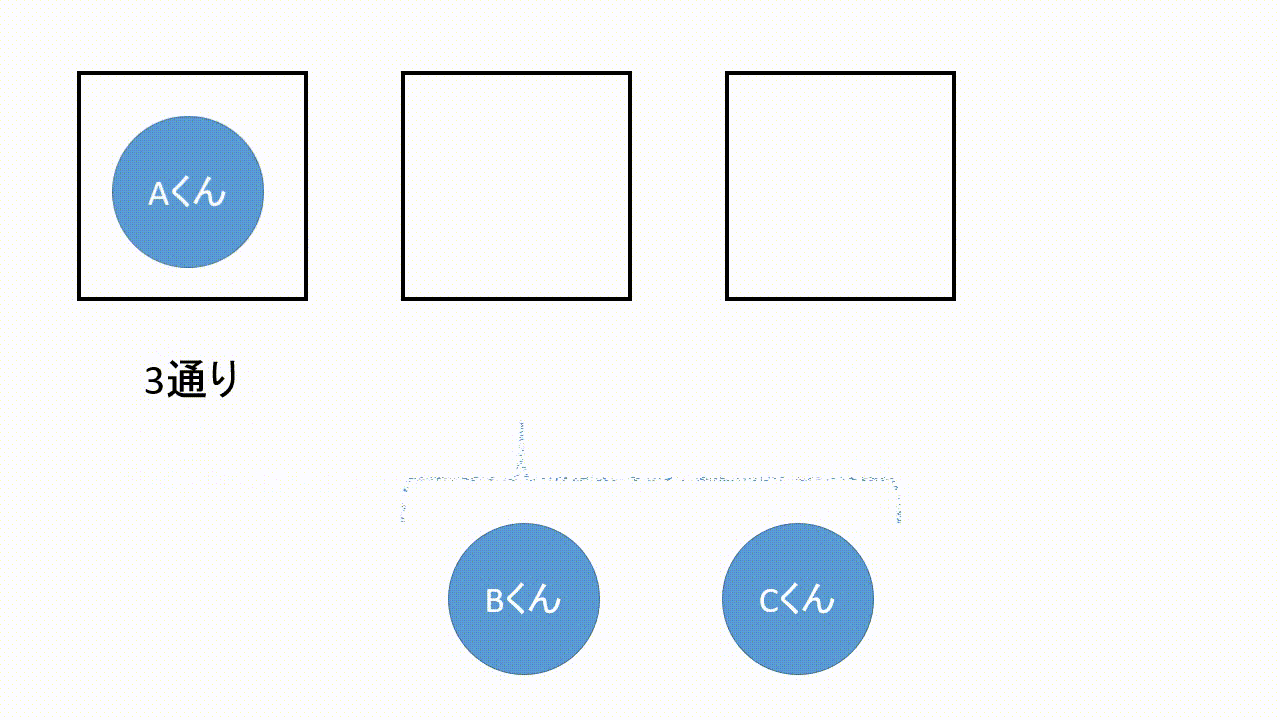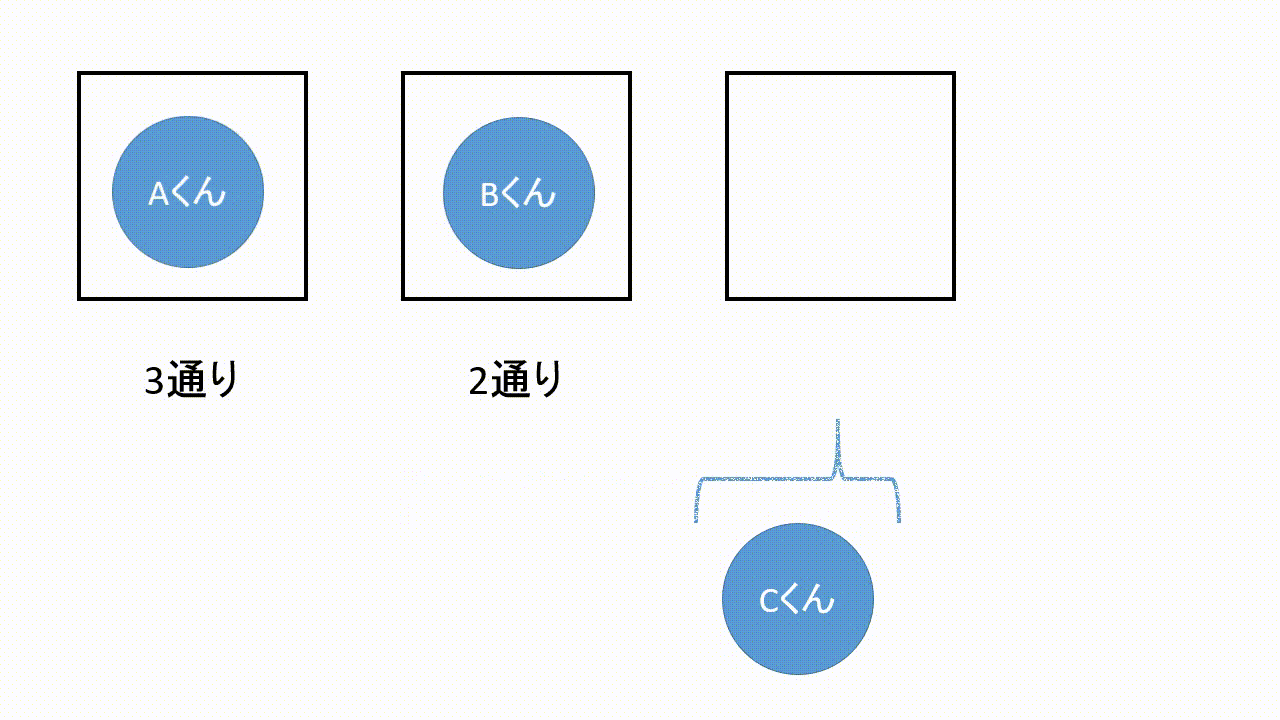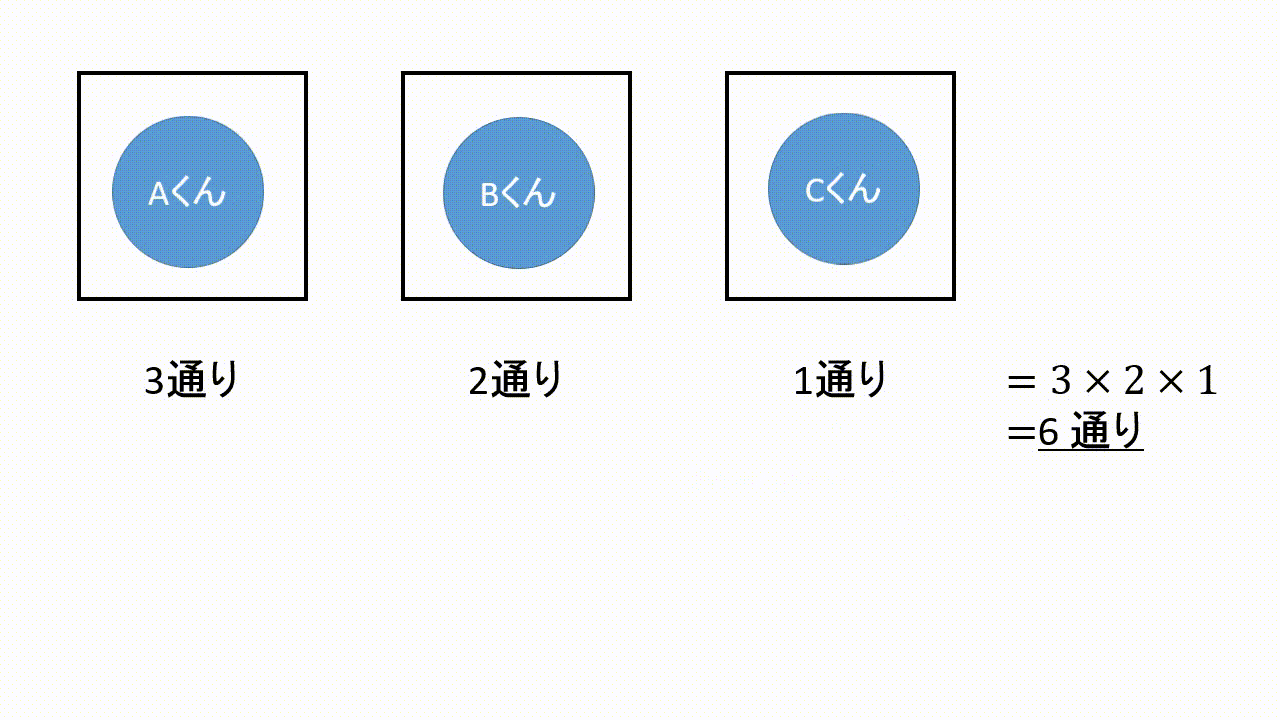
左から順に3通り，2通り，1通りと入れることができます．

ゆえに全体では

$$3通り\times2通り\times1通り=6通り$$

となります．

【2】A，B，C，D，E，Fの6人の中から2人の委員を選ぶとき，選び方は何通りあるか．^*1

よってすべての順列とカブりのものを求めると

$$\begin{eqnarray*}&&(すべての順列)=6通り\times 5通り=30通り\\&&(カブりもの)=2通り\times 1通り=2通り\end{eqnarray*}$$

したがってカブりものを取り除くと

$$\begin{eqnarray*}(組み合わせ)&=&\frac{(すべての順列)}{(カブりもの)}\\&=&\frac{30通り}{2通り}\\&=&15通り\end{eqnarray*}$$

ゆえに15通りとなる．

「場合の数」を使って「確率」求めよう！

確率は場合の数を以下のような公式に入れてあげることで求められます．

$$(事象が起こる確率)=\frac{(事象が起こる場合の数)}{(すべての場合の数)}$$

では実際に問題を解いてみましょう！

1，2，3，4，5のカードが1枚ずつある．この5枚のカードをよくきって，1枚ずつ続けて2回ひく．ひいた順に並べて2桁の整数をつくるとき，その数が偶数である確率を求めよ．^*1

よって先ほど紹介した公式に代入すると

$$\begin{eqnarray*}&&\rm\frac{(偶数になる場合の数)}{(すべての場合の数)}\\&&\rm=\frac{8通り}{20通り}\\&&\rm=\frac{2}{5}\end{eqnarray*}$$

よって答えは$$\frac{2}{5}となる．$$

まとめ

以上より，場合の数を極めてしまえば確率簡単に解くことができます．

場合の数は「書き出し」と「計算」による2つの方法で求めることができます．もちろん書き出すときは辞書順・アルファベット順のように工夫をしてあげましょう．

そして確率は上記で紹介した公式に当てはめることで簡単に求めることができます．

たくさん問題に触れて慣れていきましょう！

引用文献

1. 新中学問題集　数学2　Second Edition より