今回は中学数学のヤマ。証明問題の解き方についてコツを紹介していきます。証明問題のコツ4ポイントについて説明します。
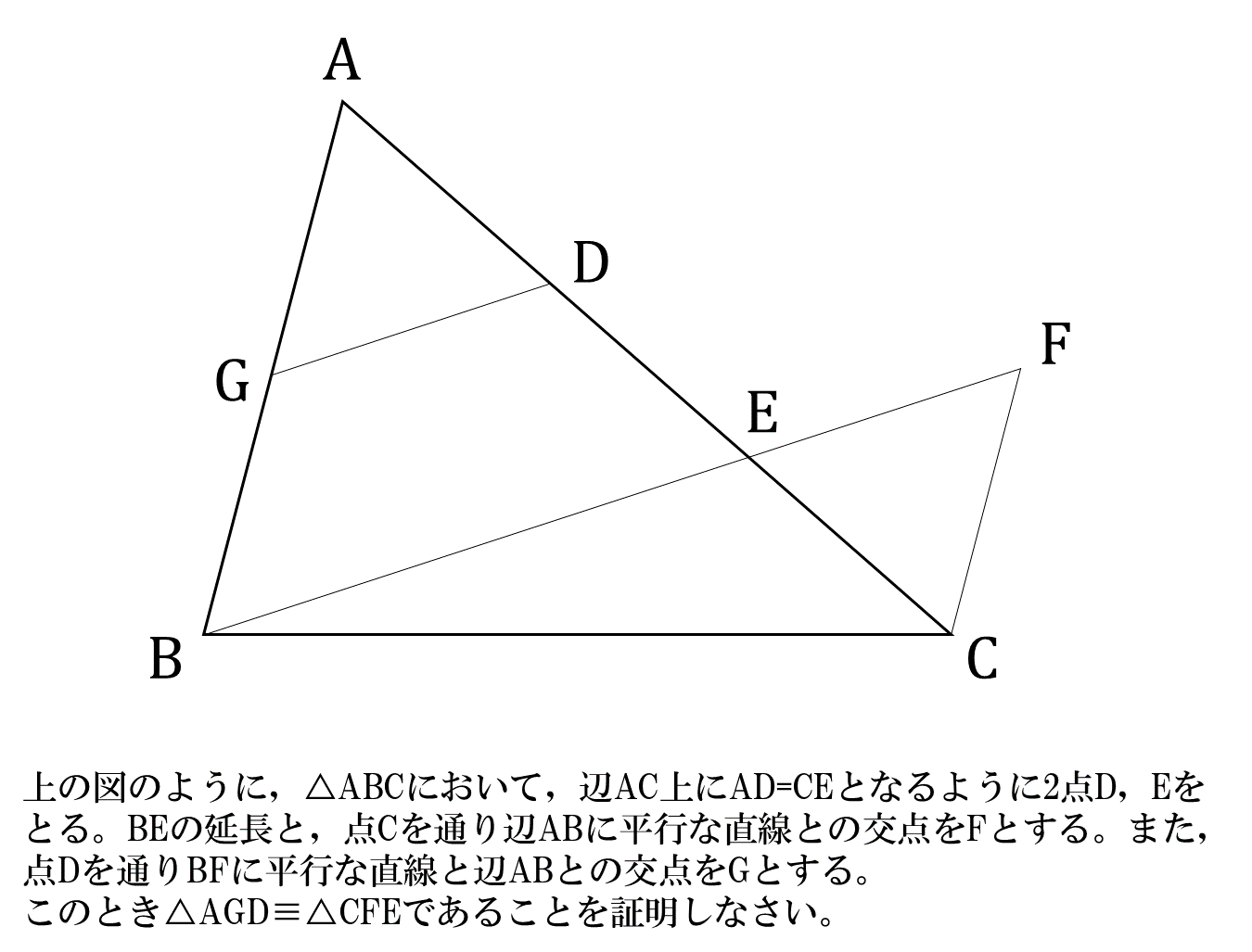
次の問題を例に4ポイントを確認してみましょう。
Contents
1.図形の性質や条件をとにかく覚える
- 三角形の合同条件
- 三角形の相似条件
- 平行線の性質
- 平行四辺形になる条件
- 直角三角形の合同条件
- 二等辺三角形の性質
など
これが何よりも大事といっても過言ではありません。
証明問題において、図形の性質や条件が決め手となります。
しかし、それらは実際のテスト本番で思いつくことができないので、覚えていなければ致命的になってしまいます。(ほとんど点数は来ないと思ってください。)
なので、とにかく図形の性質・条件を覚えてお経のように唱えられるようになる!!これに尽きます。
【この例題では】
まず、「AB∥CF」「GD∥BF」と書いてあるので、平行線の性質が使えそうです。
平行線の性質としては「①同位角が等しい」「②錯角が等しい」がありましたね。
2.「仮定」と「結論」を探してチェック、「条件」は図に書き込む
ここでの「仮定」は「AD=CE」「AB∥CF」「GD∥BF」です。「仮定」は出題者が一方的に決めている条件で、図だけからは分からないので、しっかりと確認しましょう。
またここでの「結論」は「△AGD≡△CFEを証明する」です。数学の問題全般に言えることですが、「結論=求めたいもの」は求める過程で大きなヒントとなることが多いです。なので忘れることなく、常に意識しておく必要があります。
条件はどんどん図に書きこんで(下図の赤線のように)、一目で分かるようにすることが大切です。
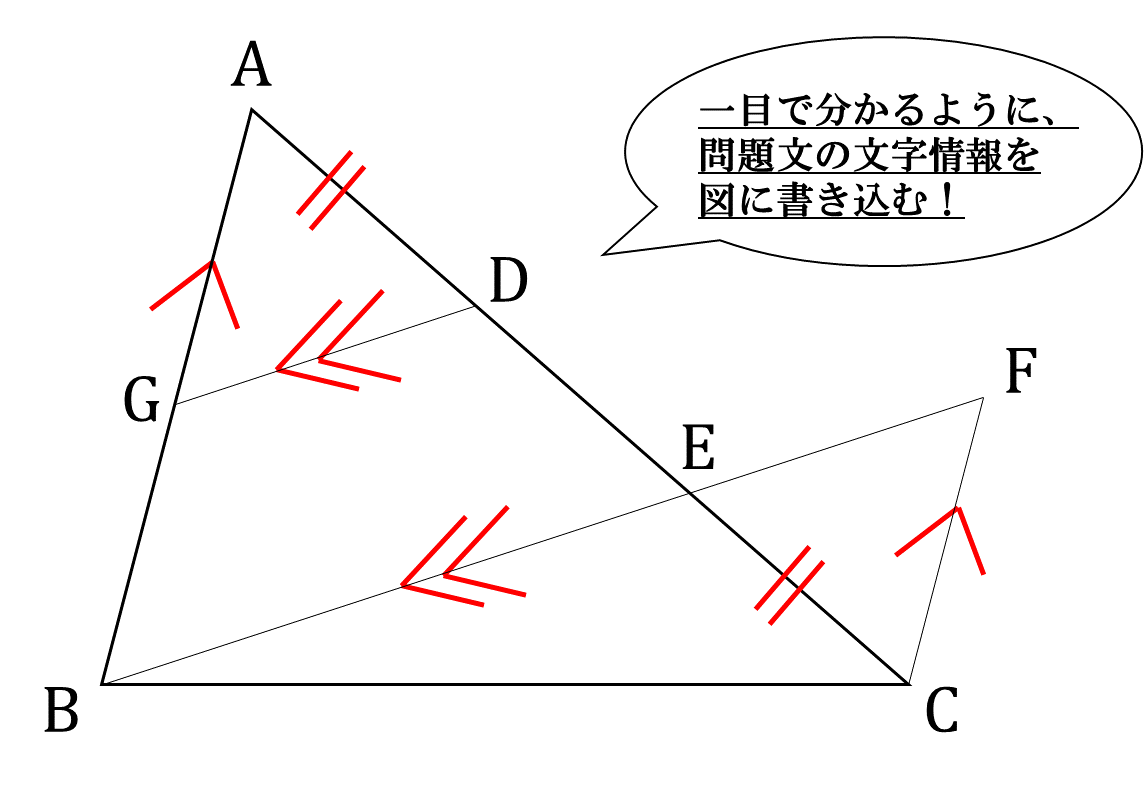
3.結論を見て、覚えた図形の条件のどれを使うか決める
図形の条件とは「三角形の合同条件」「三角形の相似条件」のことです。
問題文の仮定、結論、図をじっくりみてどの条件を使うか考えましょう。
【この例題では】
2でも書いた通り、結論は「△AGD≡△CFE」、仮定は「AD=CE」「AB∥CF」「GD∥BF」ですよね。
まず合同を証明するので、
①3辺がそれぞれ等しい
②2辺とその間の角がそれぞれ等しい
③1辺とその両端の角がそれぞれ等しい
の三つのどれかとなります。
次に仮定を見ると、「AD=CE」「AB∥CF」「GD∥BF」で、
1でも書いたように、平行線の性質から「同位角や錯角が等しいこと」が分かるから、
「角」の条件を使うという予測が立ちます。
そして上の3つの合同条件と見比べて、「③1辺とその両端の角がそれぞれ等しい」を使おう、と決まります。
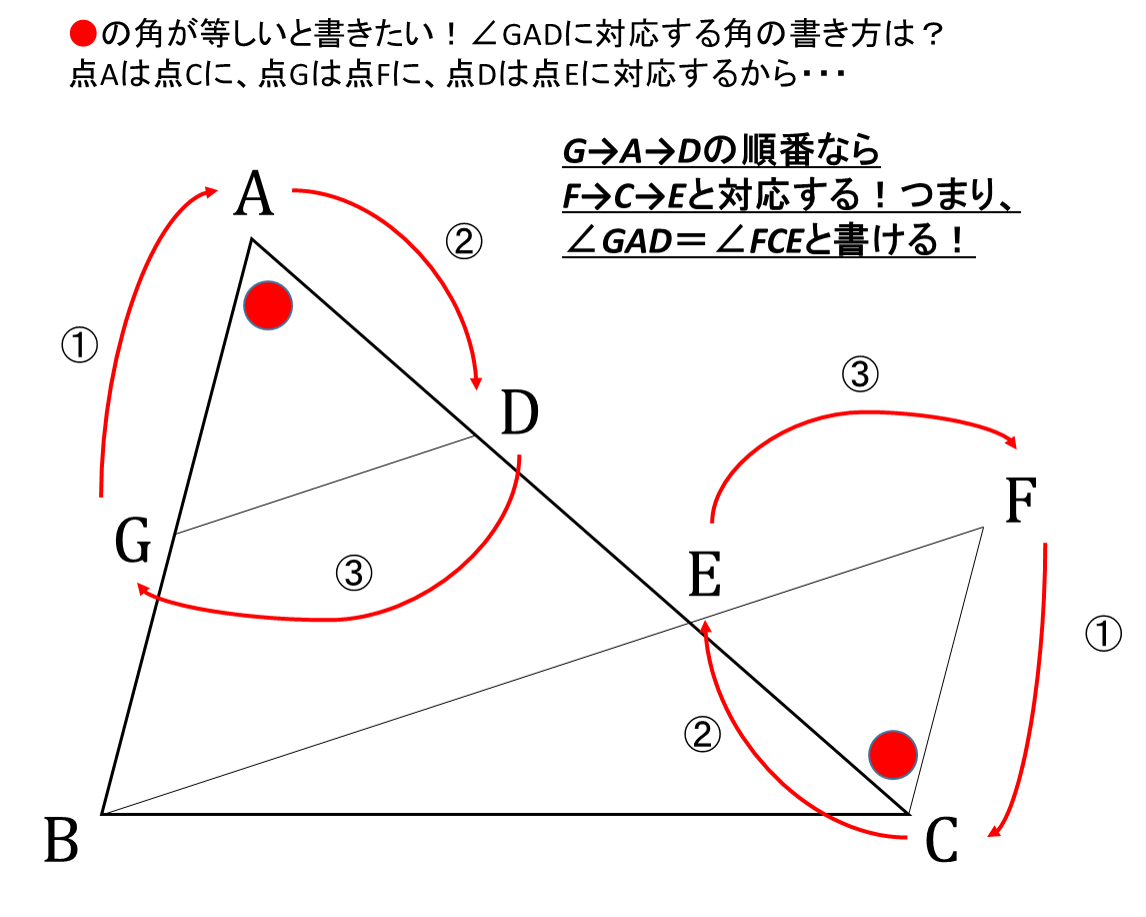
4.アルファベットが対応しているか確認する
ここでは「∠GAD=∠FCE(錯角)」の条件を使いますが、このアルファベットの並び方は証明する図形の点の並び方と一致していなければなりません。
「△AGD≡△CFE」を示すので、点Aは点Cに、点Gは点Fに、点Dは点Eに対応します。
「∠GAD=∠ECF」は数学的な意味では「∠GAD=∠FCE」と同じですが、証明の記述としては間違いとなるので注意しましょう。