Contents
都立日比谷の大問4を解く上でのポイント
- 空間図形の切り取り
- 空間図形を展開する能力
が重要です.
〔問1〕この問題は1,2分で解けるようにしましょう!
三角錐の表面積を求める問題はそれぞれの三角形の面積を求め,最後に足します.
問題を読み取るとわかるように,この三角柱には直角三角形がたくさんありますのでそれぞれの三角形の面積は簡単に求めることができます.
△BCDはDC=6, CB=8, BD=10より三平方の逆の定理より∠BCD=90°になります.これを踏まえると
△ABC,△ABD,△BCDの3つは直角三角形なので,以下のように求めることができます.
$$\rm△ABC=AB\times BC\times\frac{1}{2}\\=6\times8\times\frac{1}{2}=24[cm^{2}]$$
$$\rm△ABD=AB\times BD\times\frac{1}{2}\\=6\times10\times\frac{1}{2}=30[cm^{2}]$$
$$\rm△BCD=BC\times CD\times\frac{1}{2}\\=8\times6\times\frac{1}{2}=24[cm^{2}]$$
最後に△ACDの面積を求めます.△ACDは△ABDと辺ADを共有していることから
△ACD≡△ABD(3辺の長さが等しいため)よって面積は
$$\rm△ACD=△ABD=30[cm^{2}]$$
ゆえに三角錐の表面積は
$$\rm(三角錐の表面積)\\=△ABC+△ABD+△BCD+△ACD\\=108[cm^{2}]$$
〔問2〕計算が多いため7分程度でできると良いです!途中式も!
立体FG-HCDIをどのようにして求めるかがポイントです.
【ヒント】
立体FG-HCDIは三角錐の体積から周りを引くことで体積を求めることができます.
【詳しい解説】
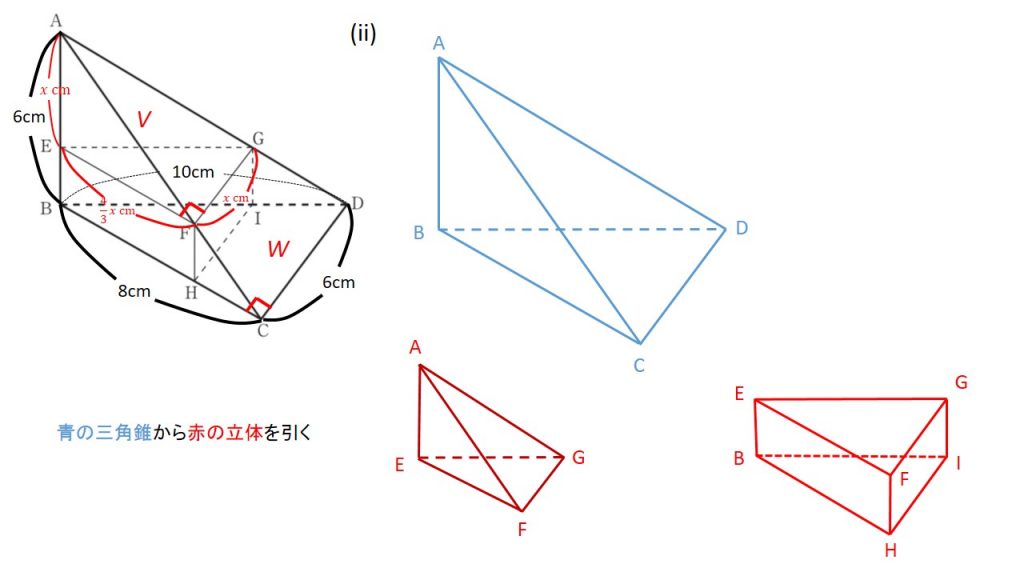
(i) 立体A-EFGの体積Vを求めていきます.
立体EFG-BHIが三角柱であることから辺EFと辺BCは平行であり,辺FG//辺CD,辺GE//辺DB.
△AEF∽△ABC,△AFG∽△ACD,△AEG∽△ABD,△EFG∽△BCDとなるので
立体A-EFG∽立体A-BCDという関係が成り立ち,相似比は
$$(立体\rm A-EFG):(立体\rm A-BCD)=\it x\rm:6 ・・・①$$
立体A-BCDの体積を求めれば立体A-EFGの体積Vも体積比を利用すれば求まります.
$$\rm(立体A-BCD)\\=BC\times CD\times\frac{1}{2}\times AB\times\frac{1}{3}\\=8\times6\times\frac{1}{2}\times6\times\frac{1}{3}\\=48[\rm cm^{3}]$$
$$\rm(立体A-EFG)\\=48[cm^{3}]\times(\frac{\it x\rm}{6})^{3}\\=\frac{2}{9}\it x\rm^{3}[cm^{3}]$$
(ii) 次に立体FG-HCDIの体積Wを求めていきます.
立体FG-HCDIは【ヒント】にあるように周りから引くことで求めることができます.
三角錐A-BCDから立体A-EFGと三角柱EFG-BHIを引けば立体FG-HCDIが求まることがわかります.
三角柱EFG-BHIの底面BHIの面積を求めていきます.
△BHIは△BCDと相似であるため直角三角形です.つまり辺BHと辺HIの長さがわかれば面積がわかります.このときの相似比は①の相似比と等しい.
$$\rm (BH:BC=)BH:8=\it x\rm:6\\BH=\frac{4}{3}\it x\rm[cm]$$
$$\rm (HI:CD=)HI:6=\it x\rm:6\\HI=\it x\rm[ cm]$$
また三角柱EFG-BHIの高さはEB=(6-x)[cm]となります.
ゆえに立体FG-HCDIの体積Wは次のようになります.
$$\rm(立体FG-HCDI)\\=(三角錐A-BCD)-((立体A-EFG)+(三角柱EFG-BHI))\\=48-((\frac{2}{9}\it x\rm^{3})+(BH\times HI\times\frac{1}{2}\times EB))\\=48-((\frac{2}{9}\it x\rm^{3})+(\frac{4}{3}\it x\rm\times\it x\rm\times\frac{1}{2}\times(6-\it x\rm)))\\=48-(-\frac{4}{9}\it x\rm^{3}+4\it x\rm^{2})$$
ゆえに問題はV:W=1:2なので(i), (ii)で求めたそれぞれの体積を代入し,xを求めます.
$$V:W=\frac{2}{9}x^{3}:48-(-\frac{4}{9} x^{3}+4x^{2})=1:2\\\frac{4}{9}x^{3}=48+\frac{4}{9}x^{3}-4x^{2}\\4x^{2}=48\\x^{2}=12 (0<x<6より)\\x=2\sqrt{3}[\rm cm]$$
〔問3〕この問題は最短の線lが思いつけば簡単!ポイントは点Q!
EP+PQ=lがどのように描かれるか考えれば展開図が描け,長さが求まります.
【ヒント】
点Qが辺CD上のどこに位置するか考えてみましょう.点Pは考える必要はあまりいりません.
【詳しい解説】
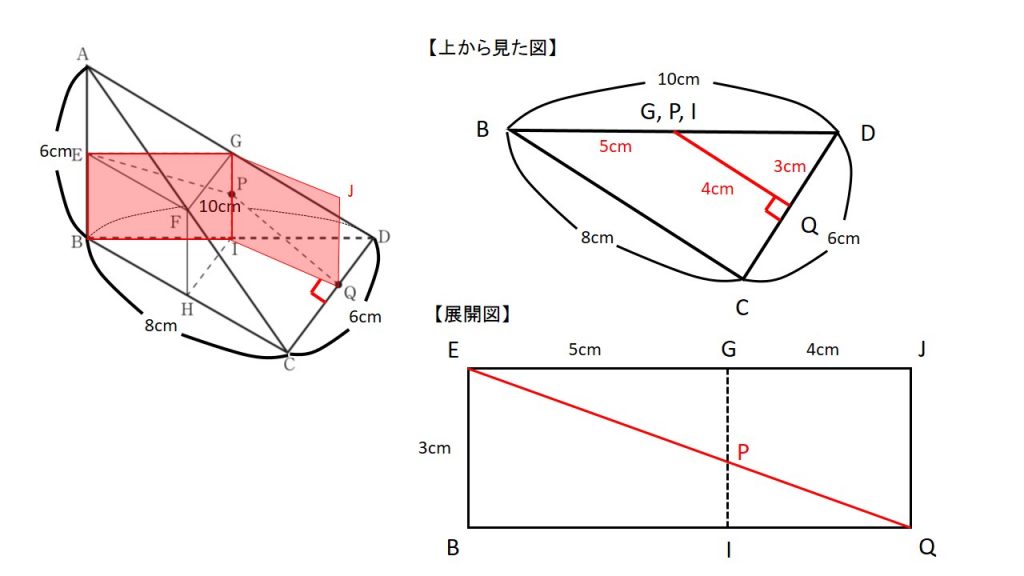
この空間図形を上から見たときの図を表すと点Qの位置するべきところがわかると思います.
EP+PQが最短になるためには点QはPQ⊥CDであることが考えられます.
$$x=3[\rm cm]$$
であることから①より辺BI=辺EG=5cmとなります.
上から見た図とその時の展開図は上図のようになります.
ゆえにEP+PQ=lの長さは
$$\rm EP+PQ=\it l\rm\\=\sqrt{EB^{2}+EJ^{2}}\\=\sqrt{3^{2}+9^{2}}\\=3\sqrt{10}[cm]$$
引用文献
- グループ作成問題*東京都立日比谷高等学校
URL:http://www.hibiya-h.metro.tokyo.jp/html/jikoumondai.html