勉強と言っても「予習」「復習」「問題演習」などありますよね。さて、この中でもどれを一番重視するべきでしょうか?
それは、「復習」です。
もちろん、授業をサラッと理解するための「予習」、解答力を付けるための「問題演習」も大事です。しかし、何よりも重要なのは「復習」です。なぜ復習がそんなに重要か、また、復習と言っても、実際どうやってやればいいの?という疑問にお答えしていこうと思います。
Contents
なぜ復習が重要か
まず、なぜ復習が重要かについて考えてみましょう。
例えば、数学で解けない問題があり、その問題の解説を学校や塾で聞いたとしましょう。その授業を受けて、公式を暗記していなかった、とか、考え方が思いつかなかった、などその問題が解けなかった原因が分かると思います。
ここで、家に帰って復習せずに、授業で学んだことを放置したとしたらどうなるでしょうか?
翌週にはその内容を忘れてしまっているでしょう。その問題に似た問題に次出会ったとき、「この問題、解けない」と繰り返すのですか?「忘れることなんてない」だって?いえ、忘れますよ。人間ですから。(笑)
それが本当にもったいない。復習していれば解けた問題だったかもしれませんよね。
その似た問題が家での演習中に解けなかったなら、まだいいです。その似た問題が出たのが高校入試本番だったとしたらどうでしょうか?「あの問題が解けていれば・・・」ってなるなんて想像するだけで怖い。でも高校入試はそういうことがザラに起こりうるのです。
というわけで、まとめると、
復習は「似た問題が次に出たとき(入試本番だと思え!)で解けるようになる」ためには必須なのです。
授業や演習、模試など、問題に取り組む機会はふんだんにあると思います。そのたびに復習して、しっかりと授業の内容やなぜできなかったのか、などを把握することが、得点アップ、からの合格に直結します。
それでは、復習の重要性が分かったところで、「じゃあ、一体具体的にはどんな感じで復習すればいいの?」という疑問にお答えしていこうと思います。
どう復習すればいいのか
それでは具体的に、どのように復習していけばいいのか考えてみましょう。
復習と言っても「授業の復習」と「問題演習(模試含む)の復習」の二つで基本的なやり方は同じなのですが、少し違う部分もあるので、それぞれについて書いていこうと思います。
授業の復習
まず、授業をしっかりと聞く、ということはもちろん大前提となります。授業中寝ていたり、ぼーっとしていたり、他のことをしていたりしていると、家に帰って授業を振り返ろうにも無理ですよね。
授業をしっかりと聞く、というのは、先生の言っている内容をちゃんと聞くということはもちろん、ノートをきれいにわかりやすく取るということでもあります。
また、板書された内容だけでなく、先生が口頭で言った内容や自分が思ったこと(疑問点、自分なりの解釈など)をメモしておくことをおすすめします。先生が言ったジョークや語呂などもメモっておくと意外といいですよ(笑)
きれいに板書を取りメモを取ることで、後で見直したときに、授業を頭の中でなるだけ近く再現できるようになります。
さて授業の復習ですが、自分のノートやテキストを授業を思い出しながら、はじめからしっかりと目を通していきます。授業中に問題を解いたなら、その問題も再度解きなおしましょう。そのときに何もつまることなくすべて理解できていれば無事終了です。
気を付けたいのは、少しでもつまづいた、または、理解できないところがあった場合です。その場合、どうしてつまづいたのか、どうして理解できないのか、ということをしっかり考えてください。ここに時間をかけることは大切です。
どうしても分からないなら、いち早く友達や先生に聞いて解決しましょう。時間を空けると何が分からなかったのかが不明になってしまいます。
一番してほしくないのが、分かったつもりになって考えるのを投げてしまうことです。
「多分こう考えるんだろ」「まあ理由は分からないけど、この流れを丸暗記しておけばいいでしょ」といった考えは禁物です。それは何も分かってません。そこで考えた分が自分の糧(かて)となると思って、めげずにしっかりと取り組んでほしいです。
問題演習の復習
次に問題演習(模試含む)の復習についてみていきましょう。
問題演習の復習で見るべき問題は基本的には丸がついてない問題だけです。
ただし、丸がついている問題でも「なんとなくやったらできちゃった」という問題もありますよね。そのような問題は次出たとき解けないという可能性がかなりあるのでしっかり復習しておく必要があります。実際そういう問題が一番危ない(笑)
このような問題は、実際に解いているときに「あれ、これよく分かんないけど解けちゃったなあ」と思ったはずなので、問題を解いているときに印をつけておいて復習時に見落としてしまわないようにしましょう。
手順① なぜ解けなかったのか解析せよ!
さて、まずやるべきことはなぜ解けなかったのかを解析することです。
大体、
- ①そもそもその分野を忘れていた(答えを見ても分からない
- ②単に公式を覚えていなかった
- ③考え方が思いつかなかった(答えを見れば分かる)
の3つに分かれると思います。
①の場合、基本の基本、教科書とノートに戻りましょう。友達や先生に直接教えてもらうのもいいでしょう。分野が分かってないならそれが解けないのは当たり前です。
②の場合、死ぬ気でその公式を覚えましょう。紙に書いてトイレなど家中に貼るなんてのでもいいです。実際、高校受験、大学受験時代の我が家のトイレには暗記事項の紙が大量に貼られていました(笑)
③の場合、これが一番多いのではないかと思います。「こんなの思いつかねーよ!」っていう気持ち、分かります(笑)しかし、実際ひらめきに頼るような問題はほとんどありません。(まれにありますが、それは諦めてもいいと思います。ほとんどみんな解けませんから。)
以下では③の場合について詳しく見ていくこととします。
その問題の解説を読んでいるとき、つまづいた部分(考え方を思いつかなかった部分)が見つかりますよね。
そのとき、その思いつかなかった部分を丸暗記することだけは絶対にやめてください。丸暗記しても「その問題」しか解けるようになりません。すこし形を変えられたり、応用されたりすると解けなくなってしまうようでは意味がない。
じゃあ、どうすればいいのか。
それはそのつまづいた部分について「どうしてその考え方になるのか」をしっかり考えることです。
すこし抽象的で分かりにくいかもしれません。 例を挙げて説明しようと思います。
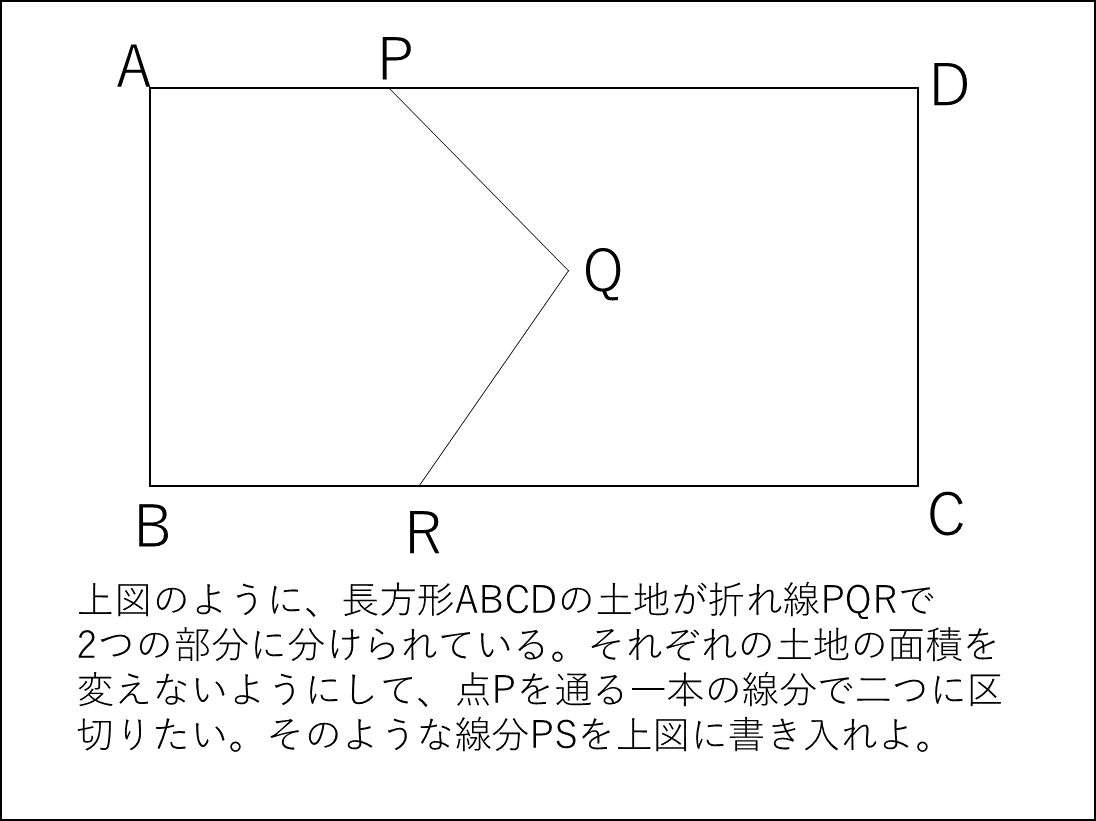
中学二年生で扱う、等積変形の定番問題です。苦手な人が意外と多いのではないでしょうか?
解答は以下のようになります。
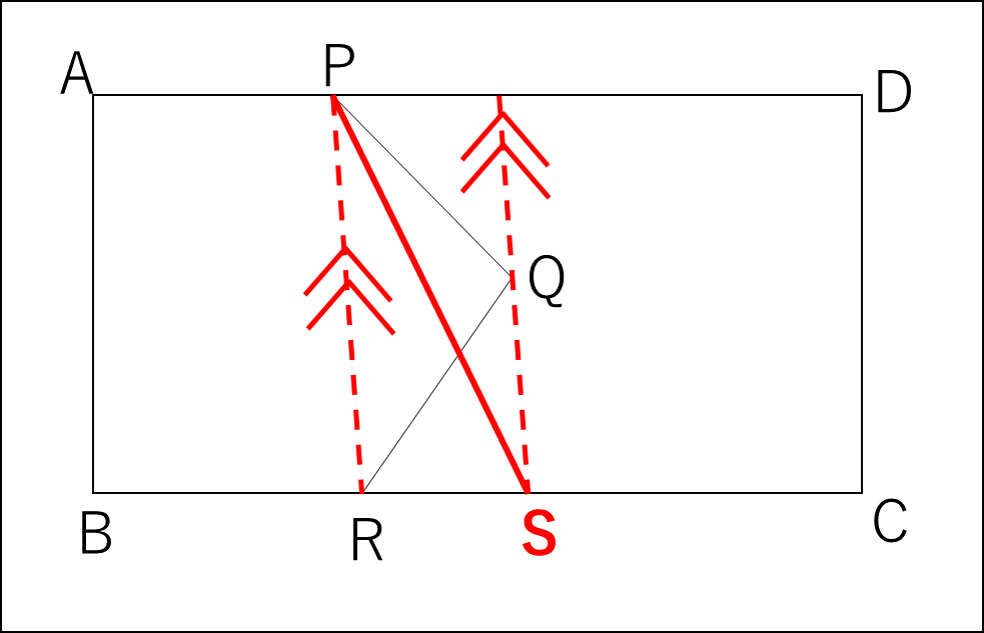
解説には、
「点Pと点Rを線分で結び、それに平行で点Qを通る直線を引く。その直線と辺BCの交点が点Sである。」
と書いてあります。
なぜそのように点Sを取り、PSを結べば、それが求めたい線分PSになるのでしょうか?
これを考えることが大事であり、解けなかった人はそれを考えることが復習です。
この問題では下のような性質を用いてますよね。
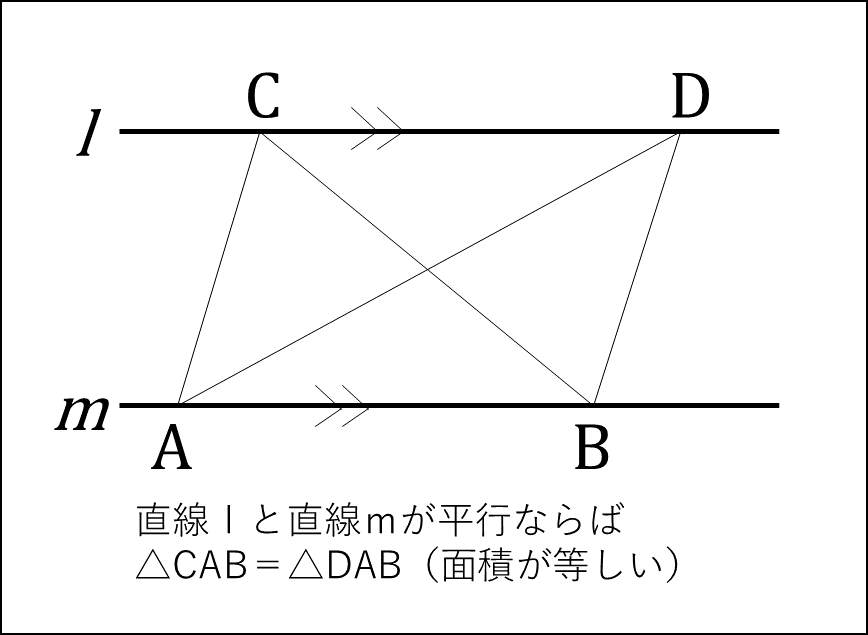
つまり、左側の土地(五角形ABRQP)を四角形ABRPと△PRQに分割し、四角形ABRPは固定、△PQRを上の性質から等積変形してあげればいいわけですよね。だから、
PRに平行で点Qを通る直線を引き、その直線と辺BCの交点をSとすれば、PRとQSは平行だから△PQR=△PRS。したがって、五角形ABRQP=四角形ABRP+△PQR=四角形ABRP+△PRS=四角形ABSP
となるわけです。
いかがでしょうか?ちゃんと上のことを考えながら解いているでしょうか?線分PS自体が引けた人でも、何も考えず機械的に解いちゃっていませんか?
面倒くさいように見えるかもしれませんが、こういった細かいことの積み重ねが問題が解けるようになり、引いては合格へと直結します。
面倒くさがらず、つまづいた部分について「なぜその考え方になるのか」をしっかりと考えるくせを付けていきましょう。
手順② 間違えた問題を何回も解きなおせ!
次にやるべきことは、「間違えた問題を時間を空けて何回も解きなおせ!」です。
やはりどんなに頑張っても人間は忘れてしまう生き物です。そのため、問題の復習は一度だけでなく、何度も繰り返して完全に頭に定着させてほしいです。
例えば、あるテストがあったとしましょう。
まず復習一回目は「テスト当日」。一回目の復習はその日にやるのが一番!当日にできなくても、二日後以内には終わらせてほしいです。
復習二回目は「テストから一週間後」。一回目の復習で学んだことを思い出しつつ解きなおしていってください。
復習三回目は「テストから三週間後or一か月後」。ここでしっかり解ければ、完全に定着できているといっていいでしょう。
最低でも復習はこの三回はしてほしいです!
何度も繰り返すようですが、毎回の復習で重視すべきは「どうしてその考え方になるのか」を考えることです。
解法の丸暗記はやめてください!(三回もやれば嫌でも解法を覚えてしまいますけど(笑))
模試の扱いについて
模試とは「模擬試験」の略ですよね。そんなの知ってるって?すみません。
私が声を大にして言いたいのは「模試・テストの復習をしっかりやれ!!!」です。
上にも書いた通り、「模擬試験」すなわち本番の試験を「真似したもの」なわけです。ということは、模試に出題された問題は、過去の傾向をもとにした本番に出やすいような問題、というわけです。
つまり、模試でできなかった問題をしっかり復習することが合格に直結するわけです。逆に言えば、模試でできなかった問題を放置すれば、本番の点数も期待できない。
だから、模試の復習に関しては、授業や問題演習の復習以上に重きを置いて取り組んでほしいと思います。
おわりに
いかがでしょうか。だいぶ長くなってしまいましたが、エッセンスはすべて詰め込まれています。上に書いたことをしっかり実行すれば確実に点数は上がると思いますので、ぜひ実行してみてください!